ГДЗ по Геометрии 10 класс Номер 300 Атанасян — Подробные Ответы

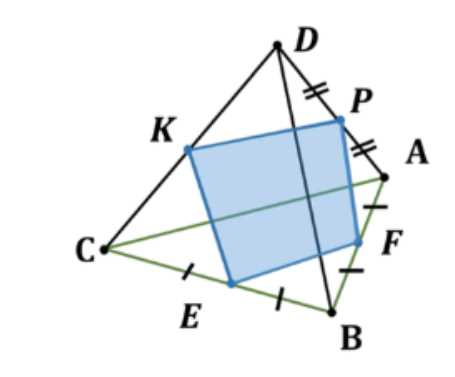
В правильной треугольной пирамиде \(DABC\) точки \(E\), \(F\) и \(P\) — середины сторон \(BC\), \(AB\) и \(AD\). Определите вид сечения, проходящего через эти точки, и найдите его площадь, если сторона основания пирамиды равна \(a\), боковое ребро равно \(b\)

По условию \(EF\) — средняя линия \(\triangle ABC\), поэтому \(EF = \frac{a}{2}\) и \(EF \parallel AC\). Аналогично \(PF = \frac{b}{2}\) и \(PF \parallel BD\). Так как \(KP\) — средняя линия \(\triangle ADC\), то \(KP = \frac{a}{2}\) и \(KP \parallel AC \parallel EF\). В правильной пирамиде \(BD \perp AC\), значит \(PF \perp EF\). Таким образом, \(KPFE\) — прямоугольник с площадью \(S_{KPFE} = \frac{a \cdot b}{4}\).

Ответ: \(KPFE\) — прямоугольник, \(S_{KPFE} = \frac{a \cdot b}{4}\).

Дано: \(ABCD\) — правильная пирамида, \(DP = PA\), \(AF = FB\), \(CE = EB\), \(AB = a\), \(AD = b\). Требуется найти тип сечения \(EPF\) и его площадь \(S_{EPF}\).

По построению \(EF\) — средняя линия \(\triangle ABC\), следовательно:
\(EF = \frac{AC}{2} = \frac{a}{2}, \quad EF \parallel AC\)

Аналогично, \(PF\) — средняя линия \(\triangle ABD\), поэтому:
\(PF = \frac{BD}{2} = \frac{b}{2}, \quad PF \parallel BD\)

Заметим, что существует единственная прямая, проходящая через точку \(P\), параллельная \(EF\), так как все четыре точки лежат в одной плоскости.

Если \(CK = KD\), то \(KP\) — средняя линия \(\triangle ADC\):
\(KP = \frac{AC}{2} = \frac{a}{2}, \quad KP \parallel AC \Rightarrow KP \parallel EF\)

Таким образом, сечение проходит через середину стороны \(CD\), и \(KPFE\) — параллелограмм.

По свойству правильной пирамиды: противоположные ребра перпендикулярны, то есть \(BD \perp AC\). Следовательно:
\(PF \perp AC \Rightarrow PF \perp EF\)

Отсюда следует, что \(KPFE\) — прямоугольник. Его площадь равна:
\(S_{KPFE} = PF \cdot EF = \frac{a}{2} \cdot \frac{b}{2} = \frac{a \cdot b}{4}\)

Ответ: сечение \(KPFE\) — прямоугольник, его площадь \(S_{KPFE} = \frac{a \cdot b}{4}\).