Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 295 Атанасян — Подробные Ответы
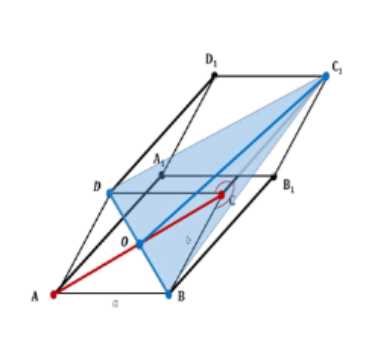
Основанием наклонного параллелепипеда \(ABCDA_1B_1C_1D_1\) является ромб. Боковое ребро \(CC_1\) составляет равные углы со сторонами основания \(CD\) и \(CB\). Докажите, что:
а) \(CC_1 \perp BD\);
б) \(BB_1D_1D\) — прямоугольник;
в) \(BD \perp AA_1C_1\);
г) \(AA_1C_1 \perp BB_1D_1\).
Дано: \(ABCDA_1B_1C_1D_1\) — наклонная призма, \(ABCD\) — ромб, \(\angle C_1CD = \angle C_1CB\).
Доказательство:
1. Проводим диагонали ромба \(AC\) и \(BD\):
\(
BD \perp AC, \quad AO = OC, \quad BO = OD \quad (*)
\)
2. Из \(\angle C_1CD = \angle C_1CB\) и \(CD = CB\) следует:
\(
\triangle C_1CD = \triangle C_1CB \Rightarrow C_1D = C_1B \quad (**)
\)
3. Из \((*)\) и \((**)\): \(C_1O\) — медиана и высота в \(\triangle C_1BD\):
\(
C_1O \perp BD \quad (***)
\)
4. а) Из \((***)\): \(C_1C \perp BD\).
5. б) Так как \(BB_1 \parallel CC_1\) и \(CC_1 \perp BD\), то \(BB_1 \perp BD \Rightarrow BB_1D_1D\) — прямоугольник.
6. в) Из \((*)\) и \((***)\): \(AA_1C_1 \perp BD\).
7. г) Из а), б), в): \(BB_1D_1 \perp AA_1C_1\).
Ответ: Что и требовалось доказать.
Дано: \(ABCDA_1B_1C_1D_1\) — наклонная призма, \(ABCD\) — ромб, \(\angle C_1CD = \angle C_1CB\).
Доказать:
а) \(C_1C \perp BD\)
б) \(BB_1D_1D\) — прямоугольник
в) \(BD \perp AA_1C_1\)
г) \(BD \perp BB_1D_1\)
Решение:
1. Проведём диагонали ромба \(AC\) и \(BD\). По свойствам ромба:
\(
BD \perp AC \quad \text{и} \quad AO = OC, \quad BO = OD \quad (*)
\)
2. По условию \(\angle C_1CD = \angle C_1CB\). Рассмотрим треугольники \(C_1CD\) и \(C_1CB\):
\(
\angle C_1CD = \angle C_1CB \quad \text{(по условию)}, \quad CD = CB \quad \text{(стороны ромба)}, \)
\(\quad C_1C \quad \text{— общая сторона}
\)
Следовательно, \(\triangle C_1CD = \triangle C_1CB\) по первому признаку равенства треугольников.
\(
\Rightarrow C_1D = C_1B \quad (**)
\)
3. Из \((*)\) и \((**)\) следует, что \(C_1O\) — не только медиана, но и высота в равнобедренном треугольнике \(C_1BD\):
\(
C_1O \perp BD \quad (***)
\)
4. Докажем пункт а):
Из \((***)\) следует, что \(C_1C \perp BD\).
5. Докажем пункт б):
Так как \(BB_1 \parallel CC_1\) (по определению призмы), а \(CC_1 \perp BD\) (из пункта а)), то:
\(
BB_1 \perp BD
\)
Поскольку \(BB_1D_1D\) — параллелограмм (так как \(BB_1 \parallel DD_1\) и \(BD \parallel B_1D_1\)), и один из его углов прямой, то \(BB_1D_1D\) — прямоугольник.
6. Докажем пункт в):
Из \((*)\) и \((***)\):
\(
C_1O \perp BD \quad \text{и} \quad AC \perp BD \quad \Rightarrow \quad AA_1C_1 \perp BD
\)
7. Докажем пункт г):
Из пунктов а), б) и в) следует, что:
\(
BB_1D_1 \perp AC \quad \text{и} \quad AA_1C_1 \perp BD \quad \Rightarrow \quad BB_1D_1 \perp AA_1C_1
\)
Ответ: Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.