
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 292 Атанасян — Подробные Ответы
В правильной четырёхугольной призме сторона основания равна 6 см, боковое ребро равно 8 см. Найдите расстояние от стороны основания до не пересекающей её диагонали призмы.
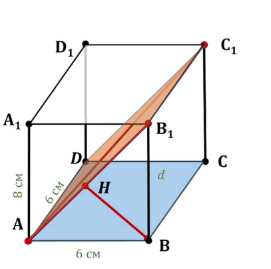
Дано: правильная призма \(ABCDA_1B_1C_1D_1\) с \(AB = 6\) см, \(AA_1 = 8\) см. Найдем расстояние между скрещивающимися прямыми \(BC\) и \(AC_1\).
Так как \(BC \parallel ADC_1B_1\) и \(AC_1 \subset ADC_1B_1\), искомое расстояние равно расстоянию от \(BC\) до плоскости \(ADC_1B_1\). Выбираем точку \(B\) и находим перпендикуляр \(BH\) в треугольнике \(ABB_1\):
1. Гипотенуза \(AB_1 = \sqrt{AB^2 + BB_1^2} = \sqrt{6^2 + 8^2} = 10\) см.
2. Площадь \(ABB_1\): \(\frac{1}{2} \cdot 6 \cdot 8 = \frac{1}{2} \cdot 10 \cdot BH\).
3. Отсюда \(BH = \frac{48}{10} = 4{,}8\) см.
Ответ: \(4{,}8\) см.
Дано: \(ABCDA_1B_1C_1D_1\) — правильная призма с квадратным основанием \(ABCD\), где \(AB = AD = 6\) см, \(AA_1 = 8\) см. Требуется найти расстояние между скрещивающимися прямыми \(BC\) и \(AC_1\).
Прямая \(BC\) лежит в плоскости основания \(ABCD\), а прямая \(AC_1\) проходит через вершину \(A\) основания и вершину \(C_1\) верхнего основания. Поскольку \(BC \parallel AD\), а \(AD\) лежит в плоскости \(ADC_1B_1\), то \(BC \parallel ADC_1B_1\). Таким образом, расстояние между \(BC\) и \(AC_1\) равно расстоянию от прямой \(BC\) до плоскости \(ADC_1B_1\), так как \(AC_1\) целиком принадлежит этой плоскости.
Для нахождения расстояния между прямой \(BC\) и плоскостью \(ADC_1B_1\) выберем удобную точку на прямой \(BC\), например точку \(B\), и найдем расстояние от \(B\) до плоскости \(ADC_1B_1\). Построим перпендикуляр \(BH\) из точки \(B\) на плоскость \(ADC_1B_1\). Так как плоскость \(ADC_1B_1\) содержит ребро \(AA_1\), то удобно рассматривать прямоугольный треугольник \(ABB_1\) в плоскости \(ABB_1A_1\), где \(BB_1 = AA_1 = 8\) см, \(AB = 6\) см.
Расстояние \(BH\) можно найти как высоту, опущенную из вершины \(B\) на гипотенузу \(AB_1\) в прямоугольном треугольнике \(ABB_1\). Длина гипотенузы \(AB_1\) вычисляется по теореме Пифагора: \(AB_1 = \sqrt{AB^2 + BB_1^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10\) см.
Площадь треугольника \(ABB_1\) можно выразить двумя способами: \(S = \frac{1}{2} \cdot AB \cdot BB_1 = \frac{1}{2} \cdot 6 \cdot 8 = 24\) см² и \(S = \frac{1}{2} \cdot AB_1 \cdot BH\). Приравнивая эти выражения, получаем: \(24 = \frac{1}{2} \cdot 10 \cdot BH\), откуда \(BH = \frac{24 \cdot 2}{10} = \frac{48}{10} = 4{,}8\) см.
Таким образом, расстояние между прямыми \(BC\) и \(AC_1\) равно \(4{,}8\) см.
Ответ: Расстояние от \(BC\) до \(AC_1\) равно \(4{,}8\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!