ГДЗ по Геометрии 10 класс Номер 29 Атанасян — Подробные Ответы

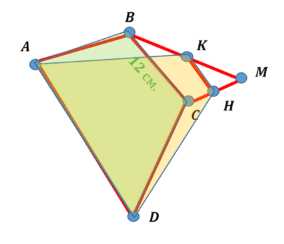
В трапеции \(ABCD\) основание \(BC\) равно \(12 \, \text{см}\). Точка \(M\) не лежит в плоскости трапеции, а точка \(K\) — середина отрезка \(BM\). Докажите, что плоскость \(ADK\) пересекает отрезок \(MC\) в некоторой точке \(H\), и найдите отрезок \(KH\).

Дано: \(ABCD\) — трапеция, \(BC \parallel AD\), \(BC = 12 \, \text{см}\), \(K\) — середина отрезка \(BM\).

Требуется доказать, что плоскость \(ADK\) пересекает \(MC\) в \(H\), и найти \(KH\).

Рассмотрим плоскость \(ADK\), которая проходит через прямую \(AD\), параллельную плоскости \(BMC\). Линия пересечения плоскостей \(ADK\) и \(BMC\) — это прямая \(KH\), которая параллельна \(AD\). Так как \(AD \parallel BC\), то \(KH \parallel BC\).

В треугольнике \(\triangle BMC\) прямая \(KH \parallel BC\). По теореме о пропорциональных отрезках: \(
\frac{KH}{BC} = \frac{BK}{BM}.
\)

Так как \(K\) — середина отрезка \(BM\), то \(BK = KM\), а значит: \(
\frac{BK}{BM} = \frac{1}{2}.
\)

Следовательно: \(
KH = \frac{1}{2} \cdot BC.
\)

Подставляя \(BC = 12 \, \text{см}\), получаем: \(
KH = \frac{1}{2} \cdot 12 = 6 \, \text{см}.
\)

Ответ: \(KH = 6 \, \text{см}\).

Дано: \(ABCD\) — трапеция, \(BC \parallel AD\), \(BC = 12 \, \text{см}\). Точка \(M\) не лежит в плоскости трапеции \(ABCD\), точка \(K\) — середина отрезка \(BM\).

Необходимо доказать, что плоскость \(ADK\) пересекает отрезок \(MC\) в точке \(H\), и найти длину отрезка \(KH\).

Решение:

1. Рассмотрим трапецию \(ABCD\), где \(BC \parallel AD\). Согласно условию, \(BC \parallel AD\), значит, эти прямые лежат в одной плоскости и параллельны (\(BC \parallel AD\)).

2. По теореме: если прямая, не лежащая в данной плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна данной плоскости. Прямая \(AD\) параллельна \(BC\), а значит, \(AD \parallel \text{плоскости } BMC\).

3. Плоскость \(ADK\) проходит через прямую \(AD\), параллельную плоскости \(BMC\), и пересекает её. Линия пересечения этих плоскостей — это прямая \(KH\), которая параллельна прямой \(AD\) (\(KH \parallel AD\)).

4. Рассмотрим треугольник \(\triangle BMC\) и прямую \(KH \parallel BC\). По теореме о пропорциональных отрезках, если прямая, параллельная основанию треугольника, пересекает две его стороны, то она делит эти стороны на пропорциональные отрезки.

5. В треугольнике \(\triangle BMC\) отрезок \(KH\) делит стороны \(BM\) и \(MC\) пропорционально. Коэффициент пропорциональности равен: \(
\frac{KH}{BC} = \frac{BK}{BM}.
\)

Так как \(K\) — середина отрезка \(BM\), то \(BK = KM\), а значит: \(
\frac{BK}{BM} = \frac{1}{2}.
\)

Следовательно: \(
KH = \frac{1}{2} \cdot BC.
\)

6. Подставляя значение \(BC = 12 \, \text{см}\), получаем: \(
KH = \frac{1}{2} \cdot 12 = 6 \, \text{см}.
\)

Ответ: точка \(H\) лежит на отрезке \(MC\), а длина отрезка \(KH\) равна \(6 \, \text{см}\).