ГДЗ по Геометрии 10 класс Номер 289 Атанасян — Подробные Ответы

Докажите, что площадь полной поверхности куба равна \(2d^2\), где \(d\) — диагональ куба.

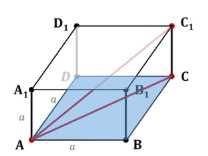
Дано: куб с ребром \(a\), диагональю \(d\). Доказать: \(S_{\text{куба}} = 2 \cdot d^2\).

Решение:
Диагональ куба: \(d = a \cdot \sqrt{3}\).
Площадь поверхности: \(S_{\text{куба}} = 6 \cdot a^2\).
Выразим \(a\) через \(d\): \(a = \frac{d}{\sqrt{3}}\).
Подставим в формулу площади:
\[
S_{\text{куба}} = 6 \cdot \left(\frac{d}{\sqrt{3}}\right)^2 = 6 \cdot \frac{d^2}{3} = 2 \cdot d^2.
\]
Что и требовалось доказать.

Решение задачи о кубе с детализацией:

Дано: куб с ребром длины \(a\). Пусть \(d\) — диагональ куба, а \(S_{\text{куба}}\) — площадь его поверхности.

Известно, что диагональ куба выражается через его ребро по формуле: \(d = a \cdot \sqrt{3}\). Это следует из теоремы Пифагора, применённой к пространственной диагонали куба, где диагональ является гипотенузой прямоугольного треугольника с катетами \(a\), \(a\sqrt{2}\) (последний — диагональ грани).

Площадь поверхности куба состоит из шести квадратных граней: \(S_{\text{куба}} = 6 \cdot a^2\).

Подставим выражение для \(a\) через \(d\) из первой формулы: \(a = \frac{d}{\sqrt{3}}\). Тогда площадь поверхности можно переписать как: \(S_{\text{куba}} = 6 \cdot \left(\frac{d}{\sqrt{3}}\right)^2 = 6 \cdot \frac{d^2}{3} = 2 \cdot d^2\).

Таким образом, доказано, что \(S_{\text{куба}} = 2 \cdot d^2\), что и требовалось.