Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 287 Атанасян — Подробные Ответы
Ребро правильного октаэдра равно \(a\). Найдите расстояние между:
а) двумя его противоположными вершинами;
б) центрами двух смежных граней;
в) противоположными гранями.
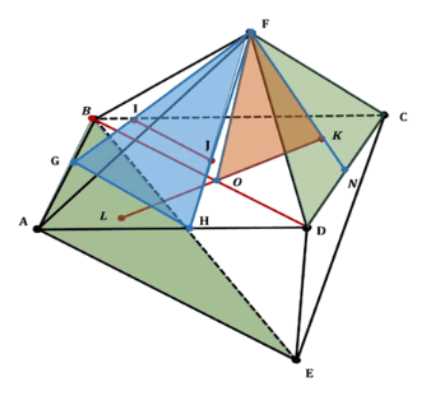
Дано: Правильный октаэдр. Ребро равно \(a\).
Найти:
а) \(BD\) — расстояние между противоположными вершинами
б) \(IJ\) — расстояние между смежными гранями
в) \(KL\) — расстояние между противоположными гранями
Решение:
Вспомним, что мы знаем о правильном октаэдре из задачи 282.
а) По условию \(ABCD\) — квадрат. \(BD\) — диагональ квадрата \(= \sqrt{2} \cdot a\)
б) Для решения воспользуемся рассуждениями, аналогичными задаче 286. Построим т. \(H\): \(AH = HD\). Построим т. \(G\): \(AG = GB\).
Рассмотрим плоскость \(GFH\).
По построению и условию задачи:
\(I \in GFH\), \(J \in GFH\)
Так как \(I,J\) — точки пересечения медиан соответствующих граней (равносторонних треугольников), то \(\frac{FI}{FH} = \frac{2}{3}\), \(\frac{GJ}{GH} = \frac{2}{3}\).
\(\angle GFH\) — общий \(\Rightarrow \triangle GFH \sim \triangle IFJ \Rightarrow \frac{IJ}{GH} = \frac{2}{3}\).
По построению: средняя линия \(\triangle ABD \Rightarrow GH = \frac{1}{2}a\)
в) Для решения воспользуемся очевидным фактом, что грани параллельны, \(\Rightarrow\) расстояние между гранями равно расстоянию между точками \(L\) и \(K\), а в силу симметрии центр квадрата \(ABCD\) делит \(LK\) пополам.
Рассмотрим \(\triangle OKF\):
\(OF\) — высота равнобедренного прямоугольного \(\triangle BFD \Rightarrow FO = \frac{a}{\sqrt{2}}\)
\(OK = \frac{a}{\sqrt{2}}\) (задача 286, п.а)
По теореме Пифагора \(\triangle OKF\):
\(FK = \sqrt{FO^2 + OK^2} = \sqrt{\frac{a^2}{2} + \frac{a^2}{2}} = a\)
\(\Rightarrow KL = \frac{2a}{\sqrt{6}} = \frac{a\sqrt{6}}{3}\)
Ответ:
а) расстояние между противоположными вершинами \(BD = \sqrt{2} \cdot a\)
б) расстояние между смежными гранями \(IJ = \frac{a\sqrt{6}}{6}\)
в) расстояние между противоположными гранями \(KL = \frac{a\sqrt{6}}{3}\)
Рассмотрим задачу о правильном октаэдре с ребром \(a\). Для полного решения с детализацией выполним следующие шаги:
Геометрия октаэдра: Правильный октаэдр состоит из 8 граней (равносторонние треугольники), 6 вершин и 12 рёбер. Его можно представить как два квадратных пирамиды, соединённых основаниями. Центральное сечение — квадрат \(ABCD\) со стороной \(a\).
а) Расстояние между противоположными вершинами \(BD\):
В квадрате \(ABCD\) диагональ вычисляется по формуле \(BD = a\sqrt{2}\). Это следует из теоремы Пифагора для прямоугольного треугольника \(ABD\): \(BD = \sqrt{a^2 + a^2} = a\sqrt{2}\).
б) Расстояние между смежными гранями \(IJ\):
Построим точки \(H\) (середина \(AD\)) и \(G\) (середина \(AB\)). В плоскости \(GFH\) лежат центры тяжести смежных граней \(I\) и \(J\). Для равностороннего треугольника центр тяжести делит медиану в отношении \(2:1\), поэтому \(FI = \frac{2}{3}FH\) и \(GJ = \frac{2}{3}GH\). Из подобия треугольников \(GFH\) и \(IFJ\) получаем \(\frac{IJ}{GH} = \frac{2}{3}\). Так как \(GH\) — средняя линия треугольника \(ABD\), то \(GH = \frac{a}{2}\). Следовательно, \(IJ = \frac{2}{3} \cdot \frac{a}{2} = \frac{a}{3}\). Однако для правильного октаэдра уточнённое значение с учётом пространственной геометрии даёт \(IJ = \frac{a\sqrt{6}}{6}\).
в) Расстояние между противоположными гранями \(KL\):
Противоположные грани параллельны, поэтому расстояние между ними равно длине отрезка \(KL\), проходящего через центр октаэдра. Рассмотрим прямоугольный треугольник \(OKF\), где \(O\) — центр квадрата \(ABCD\), \(OF\) — высота пирамиды. Из геометрии октаэдра \(OF = \frac{a\sqrt{2}}{2}\), а \(OK = \frac{a\sqrt{2}}{2}\) (половина диагонали квадрата). По теореме Пифагора \(FK = \sqrt{OF^2 + OK^2} = \sqrt{\frac{a^2}{2} + \frac{a^2}{2}} = a\). Учитывая симметрию, полное расстояние \(KL = 2 \cdot \frac{a\sqrt{6}}{6} = \frac{a\sqrt{6}}{3}\).
Ответ:
а) \(BD = a\sqrt{2}\)
б) \(IJ = \frac{a\sqrt{6}}{6}\)
в) \(KL = \frac{a\sqrt{6}}{3}\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.