ГДЗ по Геометрии 10 класс Номер 286 Атанасян — Подробные Ответы

В правильном тетраэдре \(h\) — высота, \(m\) — ребро, а \(n\) — расстояние между центрами его граней. Выразите:
а) \(m\) через \(h\);
б) \(n\) через \(m\).

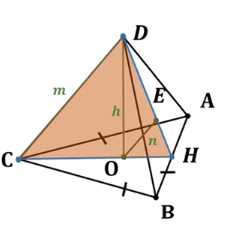
Дано: \(ABCD\) — правильный тетраэдр. \(O, E\) — центры граней \(CD = m\), \(DO = h\), \(OE = n\).
Найти:
а) \(m\) через \(h\) б) \(n\) через \(m\).

Решение:
Построим точку \(H\): \(AH = HB\).
Рассмотрим плоскость \(CDH\).
По построению и условию задачи:
\(O \in CDH\), \(E \in CDH\), \(DO \perp CH\) (*).

Так как \(O, E\) — точки пересечения медиан соответствующих граней (равносторонних треугольников), то:
\(\frac{CO}{CH} = \frac{2}{3}\), \(\frac{DE}{DH} = \frac{2}{3}\) (**).

б) Из (*) и (**), \(\angle DHC\) — общий \(\Rightarrow \triangle CDH \sim \triangle OEH\).
Следовательно:
\(\frac{OE}{CD} = \frac{EH}{DH} = \frac{1}{3} \Rightarrow n = \frac{m}{3}\).

а) \(\triangle CBH\) прямоугольный \(\Rightarrow\) по теореме Пифагора:
\(CH = \sqrt{CB^2 — BH^2} = \sqrt{m^2 — \left(\frac{m}{2}\right)^2} = \frac{\sqrt{3}}{2}m\).

Из (**): \(CO = \frac{2}{3}CH = \frac{2}{3} \cdot \frac{\sqrt{3}}{2}m = \frac{\sqrt{3}}{3}m\).

\(\triangle COD\) прямоугольный \(\Rightarrow\) по теореме Пифагора:
\(CD^2 = CO^2 + OD^2 \Rightarrow m^2 = \left(\frac{\sqrt{3}}{3}m\right)^2 + h^2\).
Упрощаем:
\(m^2 = \frac{1}{3}m^2 + h^2 \Rightarrow \frac{2}{3}m^2 = h^2 \Rightarrow m = h \cdot \sqrt{\frac{3}{2}} = \frac{h \sqrt{6}}{2}\).

Ответ:
а) \(m = \frac{h \sqrt{6}}{2}\), б) \(n = \frac{m}{3} = \frac{h \sqrt{6}}{6}\).

Решение задачи о правильном тетраэдре \(ABCD\) с центрами граней \(O\) и \(E\):

В правильном тетраэдре все грани являются равносторонними треугольниками. Пусть \(CD = m\), \(DO = h\), \(OE = n\). Рассмотрим следующие шаги:

Построим точку \(H\) как середину ребра \(AB\), тогда \(AH = HB = \frac{m}{2}\). В плоскости \(CDH\) находятся точки \(O\) (центр грани \(ABC\)) и \(E\) (центр грани \(ABD\)), причем \(DO \perp CH\).

В равносторонних треугольниках центры делят медианы в отношении 2:1. Для грани \(ABC\) имеем \(\frac{CO}{CH} = \frac{2}{3}\), а для грани \(ABD\) — \(\frac{DE}{DH} = \frac{2}{3}\).

Треугольники \(CDH\) и \(OEH\) подобны, так как имеют общий угол \(\angle DHC\) и пропорциональные стороны. Из подобия получаем \(\frac{OE}{CD} = \frac{EH}{DH} = \frac{1}{3}\), откуда следует \(n = \frac{m}{3}\).

Для нахождения \(m\) через \(h\) рассмотрим прямоугольный треугольник \(CBH\): \(CH = \sqrt{m^2 — (\frac{m}{2})^2} = \frac{\sqrt{3}}{2}m\). Тогда \(CO = \frac{2}{3}CH = \frac{\sqrt{3}}{3}m\).

Применяя теорему Пифагора к треугольнику \(COD\): \(m^2 = (\frac{\sqrt{3}}{3}m)^2 + h^2\). Упрощая, получаем \(\frac{2}{3}m^2 = h^2\), откуда \(m = \frac{h\sqrt{6}}{2}\).

Подставляя \(m\) в выражение для \(n\), получаем \(n = \frac{h\sqrt{6}}{6}\).

Ответ:
а) \(m = \frac{h\sqrt{6}}{2}\),
б) \(n = \frac{h\sqrt{6}}{6}\).