ГДЗ по Геометрии 10 класс Номер 285 Атанасян — Подробные Ответы

Докажите, что в правильном тетраэдре отрезки, соединяющие центры граней, равны друг другу.

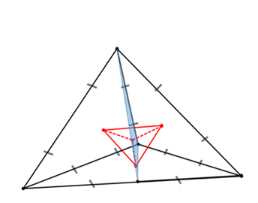
Рассмотрим правильный тетраэдр \(ABCD\). Соединим центры его граней, получив новый тетраэдр \(A’B’C’D’\). Докажем, что все его рёбра равны.

Поскольку \(ABCD\) — правильный тетраэдр, он обладает симметрией относительно плоскостей, проходящих через его высоты. Пусть \(\Pi\) — одна из таких плоскостей симметрии. Тогда вершины \(A’\) и \(B’\) симметричны относительно \(\Pi\), а вершины \(C’\) и \(D’\) лежат в \(\Pi\).

Из симметрии следует, что отрезки \(A’C’\) и \(B’C’\) равны, так как \(A’\) и \(B’\) симметричны, а \(C’\) лежит в плоскости симметрии. Аналогично, применяя рассуждения ко всем плоскостям симметрии, получаем, что все рёбра тетраэдра \(A’B’C’D’\) равны.

Таким образом, отрезки, соединяющие центры граней правильного тетраэдра, равны.

Рассмотрим правильный тетраэдр \(ABCD\) с ребрами равной длины. Нам нужно доказать, что отрезки, соединяющие центры его граней, равны между собой. Центры граней — это точки пересечения медиан соответствующих треугольных граней. Обозначим центры граней \(ABC\), \(ABD\), \(ACD\) и \(BCD\) как \(K\), \(L\), \(M\) и \(N\) соответственно.

Шаг 1: Построение нового тетраэдра. Соединим центры граней \(K\), \(L\), \(M\), \(N\) отрезками. Получим новый тетраэдр \(KLMN\). Нам нужно доказать, что все его рёбра равны, то есть \(KL = LM = MN = NK = KM = LN\).

Шаг 2: Использование симметрии. Правильный тетраэдр обладает шестью плоскостями симметрии. Каждая из них проходит через ребро и середину противоположного ребра. Рассмотрим одну такую плоскость симметрии \(\Pi\), например, проходящую через ребро \(AB\) и середину ребра \(CD\).

Шаг 3: Анализ расположения точек. В силу симметрии, точки \(K\) (центр грани \(ABC\)) и \(L\) (центр грани \(ABD\)) симметричны относительно \(\Pi\), так как грани \(ABC\) и \(ABD\) симметричны относительно этой плоскости. Точки \(M\) (центр \(ACD\)) и \(N\) (центр \(BCD\)) лежат в самой плоскости \(\Pi\), поскольку их грани симметричны друг другу относительно \(\Pi\).

Шаг 4: Доказательство равенства рёбер. Рассмотрим рёбра \(KM\) и \(LM\). Поскольку \(K\) и \(L\) симметричны, а \(M\) лежит в плоскости симметрии, отрезки \(KM\) и \(LM\) равны как симметричные относительно \(\Pi\). Аналогично, применяя те же рассуждения к другим плоскостям симметрии, можно показать, что все рёбра тетраэдра \(KLMN\) попарно равны.

Шаг 5: Обобщение. Поскольку правильный тетраэдр имеет несколько плоскостей симметрии, можно выбрать любую из них и повторить рассуждения. Это гарантирует, что все рёбра \(KLMN\) равны, а значит, отрезки, соединяющие центры граней исходного тетраэдра, действительно равны между собой.

Таким образом, мы доказали, что в правильном тетраэдре отрезки, соединяющие центры граней, равны, используя свойства симметрии и геометрические построения.