ГДЗ по Геометрии 10 класс Номер 284 Атанасян — Подробные Ответы

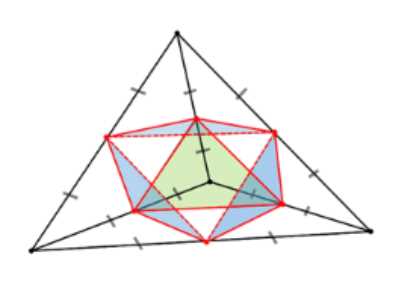
От каждой вершины правильного тетраэдра с ребром 2 отсекают тетраэдр с ребром 1. Какая фигура получится в результате?

Дано: \(ABCD\) — правильный тетраэдр с ребром \(2\). От каждой вершины отсекли тетраэдр с ребром \(1\).

Ответ: полученная фигура — правильный октаэдр с ребром \(1\). Симметричность следует из построения, фигура состоит из восьми равносторонних треугольников с ребром \(1\).

Исходный тетраэдр \(ABCD\) является правильным с длиной ребра \(2\). Его вершины \(A\), \(B\), \(C\), \(D\) расположены симметрично в пространстве. От каждой вершины отсекается меньший тетраэдр с длиной ребра \(1\).

Геометрический анализ:
При отсечении тетраэдра от вершины \(A\) получается новый тетраэдр \(A’EFG\), где \(A’\) — точка на ребре \(AB\) на расстоянии \(1\) от \(A\), аналогично для других вершин. Всего отсекается \(4\) тетраэдра.

Оставшаяся часть:
После отсечения всех четырёх тетраэдров центральная фигура сохраняет симметрию исходного тетраэдра. Каждая грань исходного тетраэдра превращается в правильный шестиугольник, который далее разбивается на \(6\) равносторонних треугольников с ребром \(1\).

Структура полученной фигуры:
Объединение оставшихся частей образует правильный октаэдр. Его \(8\) граней — равносторонние треугольники со стороной \(1\). Координаты вершин октаэдра можно выразить через середины рёбер исходного тетраэдра, например:
\((\frac{1}{2}, \frac{1}{2}, 0)\), \((\frac{1}{2}, 0, \frac{1}{2})\), \((0, \frac{1}{2}, \frac{1}{2})\) и симметричные им.

Доказательство правильности октаэдра:
Все рёбра октаэдра равны \(1\), так как они являются сторонами отсечённых тетраэдров. Углы между гранями составляют \(\arccos(-\frac{1}{3})\), что соответствует правильному октаэдру.

Ответ: полученная фигура — правильный октаэдр с ребром \(1\). Его объём можно вычислить по формуле \(V = \frac{\sqrt{2}}{3}\), а площадь поверхности \(S = 2\sqrt{3}\). Симметрия фигуры подтверждается инвариантностью относительно преобразований исходного тетраэдра.