
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 283 Атанасян — Подробные Ответы
В правильном тетраэдре \(DABC\) ребро равно \(a\). Найдите площадь сечения тетраэдра плоскостью, проходящей через центр грани \(ABC\):
а) параллельно грани \(BDC\);
б) перпендикулярно к ребру \(AD\)
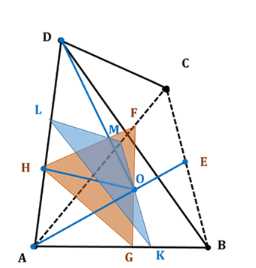
Рассмотрим правильный тетраэдр \(ABCD\) с ребром \(a\). Центр основания \(ABC\) — точка \(O\). По условию \(OH \perp AD\), \(FG \perp AD\), \(KLM \parallel ABC\).
Из подобия треугольников \(AKL\) и \(ABD\) получаем \(\frac{KL}{BD} = \frac{AK}{AB} = \frac{2}{3}\), значит \(KL = \frac{2}{3}a\). Аналогично \(KM = \frac{2}{3}a\). Площадь треугольника \(KLM\): \(S_{KLM} = \frac{1}{2} \cdot KM \cdot KL \cdot \sin(60^\circ) = \frac{1}{2} \cdot \frac{4}{9}a^2 \cdot \frac{\sqrt{3}}{2} = \frac{a^2 \sqrt{3}}{9}\).
Угол между гранью \(ABC\) и ребром \(AD\) равен \(\theta = \arcsin\left(\frac{\sqrt{6}}{3}\right)\). Тогда площадь \(S_{FGH} = S_{KLM} \cdot \cos(\theta) = \frac{a^2 \sqrt{3}}{9} \cdot \frac{\sqrt{3}}{3} = \frac{a^2}{9}\).
Ответ: \(S_{KLM} = \frac{a^2 \sqrt{3}}{9}\), \(S_{FGH} = \frac{a^2}{9}\).
Рассмотрим правильный тетраэдр \(ABCD\) с длиной ребра \(a\). Все грани такого тетраэдра являются равносторонними треугольниками, а все двугранные углы равны между собой. Обозначим центр основания \(ABC\) как точку \(O\), которая одновременно является точкой пересечения медиан, высот и биссектрис равностороннего треугольника \(ABC\).
Для нахождения площади сечения \(KLM\) сначала определим его положение в пространстве. По условию плоскость \(KLM\) параллельна основанию \(ABC\) и проходит через точку \(O\). Из параллельности плоскостей следует подобие треугольников \(KLM\) и \(ABC\). Коэффициент подобия можно определить, рассмотрев положение точки \(O\) относительно вершин тетраэдра.
В равностороннем треугольнике медианы делятся в отношении \(2:1\) от вершины. Пусть \(AK\) представляет собой отрезок от вершины \(A\) до точки \(K\) на ребре \(AD\). Тогда отношение \(AO : OK = 2 : 1\), что означает \(AK = \frac{2}{3}AD\).
Из подобия треугольников \(AKL\) и \(ABD\) выводим следующее соотношение:
\(
\frac{KL}{BD} = \frac{AK}{AB} = \frac{2}{3} \Rightarrow KL = \frac{2}{3}a.
\)
Аналогичным образом, рассматривая подобие треугольников \(AKM\) и \(ACD\), получаем:
\(
KM = \frac{2}{3}a.
\)
Так как \(KLM\) параллелен \(ABC\), угол между сторонами \(KL\) и \(KM\) составляет \(60^\circ\). Площадь треугольника \(KLM\) вычисляется по формуле площади треугольника через две стороны и угол между ними:
\(
S_{KLM} = \frac{1}{2} \cdot KL \cdot KM \cdot \sin(60^\circ) = \frac{1}{2} \cdot \frac{4}{9}a^2 \cdot \frac{\sqrt{3}}{2} = \frac{a^2 \sqrt{3}}{9}.
\)
Перейдем к рассмотрению сечения \(FGH\), которое перпендикулярно ребру \(AD\). По условию \(OH \perp AD\), а \(FG \perp AD\). Плоскость \(FGH\) перпендикулярна \(AD\), при этом линия \(FG\) параллельна стороне \(CB\) основания.
Угол между гранью \(ABC\) и ребром \(AD\) можно выразить через линейный угол соответствующего двугранного угла. Для правильного тетраэдра этот угол \(\theta\) удовлетворяет следующим тригонометрическим соотношениям:
\(
\sin(\theta) = \frac{\sqrt{6}}{3}, \quad \cos(\theta) = \frac{\sqrt{3}}{3}.
\)
Площадь сечения \(FGH\) связана с площадью \(KLM\) через косинус угла между плоскостями:
\(
S_{FGH} = S_{KLM} \cdot \cos(\theta) = \frac{a^2 \sqrt{3}}{9} \cdot \frac{\sqrt{3}}{3} = \frac{a^2}{9}.
\)
Таким образом, окончательные значения площадей сечений составляют:
\(
S_{KLM} = \frac{a^2 \sqrt{3}}{9}, \quad S_{FGH} = \frac{a^2}{9}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!