ГДЗ по Геометрии 10 класс Номер 282 Атанасян — Подробные Ответы

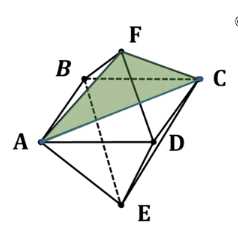
Найдите угол между двумя рёбрами правильного октаэдра, которые имеют общую вершину, но не принадлежат одной грани.

Рассмотрим правильный октаэдр. По условию \(ABCD\) — квадрат, значит \(AC\) — диагональ квадрата: \(AC = AB \cdot \sqrt{2}\). Так как \(AF = AB\) и \(CF = AB\), то \(AC^2 = 2 \cdot AB^2 = AF^2 + FC^2\). По теореме, обратной теореме Пифагора, \(\triangle AFC\) — прямоугольный, следовательно \(\angle AFC = 90^\circ\).

Ответ: \(\angle AFC = 90^\circ\).

Рассмотрим задачу о правильном октаэдре и тетраэдре \(AB_1CD_1\). По условию \(ABCD\) — квадрат, следовательно, все его стороны равны: \(AB = BC = CD = DA\). Диагональ квадрата \(AC\) вычисляется по формуле \(AC = AB \cdot \sqrt{2}\).

Точки \(B_1\) и \(D_1\) расположены так, что \(AB_1 = AD_1 = AB\) (поскольку октаэдр правильный). Аналогично, \(CB_1 = CD_1 = AB\). Таким образом, треугольники \(AB_1C\) и \(AD_1C\) являются равносторонними, так как все их стороны равны \(AB\).

Теперь рассмотрим треугольник \(AFC\), где \(F\) — вершина октаэдра. По условию \(AF = AB\) и \(CF = AB\). Подставим известные значения в выражение для \(AC^2\):
\(
AC^2 = (AB \cdot \sqrt{2})^2 = 2 \cdot AB^2
\)
С другой стороны, сумма квадратов сторон \(AF\) и \(CF\):
\(
AF^2 + CF^2 = AB^2 + AB^2 = 2 \cdot AB^2
\)
Таким образом, выполняется равенство:
\(
AC^2 = AF^2 + CF^2
\)
Согласно теореме, обратной теореме Пифагора, это означает, что треугольник \(AFC\) прямоугольный, причем прямой угол лежит при вершине \(F\). Следовательно:
\(
\angle AFC = 90^\circ
\)

Ответ: \(\angle AFC = 90^\circ\).