ГДЗ по Геометрии 10 класс Номер 281 Атанасян — Подробные Ответы

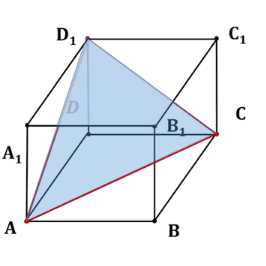
В кубе \(ABCDA_1B_1C_1D_1\) из вершины \(D_1\) проведены диагонали граней \(D_1A\), \(D_1C\) и \(D_1B_1\), и концы их соединены отрезками. Докажите, что многогранник \(D_1AB_1C\) — правильный тетраэдр. Найдите отношение площадей поверхностей куба и тетраэдра.

Дано: \(ABCDA_1B_1C_1D_1\) — куб
Доказать: \(AB_1CD_1\) — правильный тетраэдр
Найти:
\(S_{ABCDA_1B_1CD_1} = ?\)
\(S_{AB_1CD_1} = ?\)

Решение:
Рассмотрим \(AB_1CD_1\). По построению \(AB_1CD_1\) состоит из диагоналей граней куба, которые равны \(\Rightarrow AB_1 = B_1C = CD_1 = D_1A \Rightarrow AB_1CD_1\) — правильный тетраэдр. Что и требовалось доказать.

\(S_{AB_1CD_1} = 4 \cdot S_{ACD_1} = 4 \cdot \frac{\sqrt{3}}{2} \cdot AB^2\) (задача 280)
\(S_{ABCDA_1B_1CD_1} = 6 \cdot AB^2\)
\(\frac{S_{ABCDA_1B_1CD_1}}{S_{AB_1CD_1}} = \frac{6 \cdot AB^2}{4 \cdot \frac{\sqrt{3}}{2} \cdot AB^2} = \sqrt{3}\)

Ответ:
\(\frac{S_{ABCDA_1B_1CD_1}}{S_{AB_1CD_1}} = \sqrt{3}\)

Рассмотрим куб \(ABCDA_1B_1C_1D_1\), где \(ABCD\) и \(A_1B_1C_1D_1\) — его основания, а боковые рёбра \(AA_1\), \(BB_1\), \(CC_1\), \(DD_1\) соединяют соответствующие вершины. Нам нужно доказать, что фигура \(AB_1CD_1\) является правильным тетраэдром, то есть все её рёбра равны, а все грани — равносторонние треугольники.

Шаг 1: Определение рёбер тетраэдра.
Тетраэдр \(AB_1CD_1\) образован вершинами \(A\), \(B_1\), \(C\), \(D_1\). Его рёбра:
— \(AB_1\) — диагональ грани \(ABB_1A_1\),
— \(B_1C\) — диагональ грани \(BB_1C_1C\),
— \(CD_1\) — диагональ грани \(CC_1D_1D\),
— \(D_1A\) — диагональ грани \(ADD_1A_1\),
— \(AC\) — диагональ основания \(ABCD\),
— \(B_1D_1\) — диагональ верхнего основания \(A_1B_1C_1D_1\).

Шаг 2: Доказательство равенства рёбер.
Пусть длина ребра куба равна \(a\). Тогда:
— Длина диагонали грани куба: \(AB_1 = B_1C = CD_1 = D_1A = a\sqrt{2}\), так как диагональ квадрата со стороной \(a\) равна \(a\sqrt{2}\).
— Длина диагонали основания \(AC = a\sqrt{2}\) (также диагональ квадрата).
— Длина пространственной диагонали \(B_1D_1 = a\sqrt{2}\) (аналогично).

Таким образом, все рёбра тетраэдра \(AB_1CD_1\) равны \(a\sqrt{2}\), что соответствует определению правильного тетраэдра.

Шаг 3: Проверка граней.
Каждая грань тетраэдра — треугольник со сторонами \(a\sqrt{2}\), значит, все грани являются равносторонними треугольниками. Например, треугольник \(AB_1C\) имеет стороны \(AB_1 = B_1C = AC = a\sqrt{2}\).

Шаг 4: Вычисление площадей.
Площадь одной грани правильного тетраэдра со стороной \(l\) вычисляется по формуле:
\(S_{\text{грани}} = \frac{\sqrt{3}}{4} l^2 = \frac{\sqrt{3}}{4} (a\sqrt{2})^2 = \frac{\sqrt{3}}{4} \cdot 2a^2 = \frac{\sqrt{3}}{2} a^2\).

Площадь полной поверхности тетраэдра:
\(S_{AB_1CD_1} = 4 \cdot S_{\text{грани}} = 4 \cdot \frac{\sqrt{3}}{2} a^2 = 2\sqrt{3} a^2\).

Площадь поверхности куба:
\(S_{ABCDA_1B_1C_1D_1} = 6a^2\).

Отношение площадей:
\(\frac{S_{ABCDA_1B_1C_1D_1}}{S_{AB_1CD_1}} = \frac{6a^2}{2\sqrt{3} a^2} = \frac{6}{2\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3}\).

Итоговый ответ:
\(\frac{S_{ABCDA_1B_1C_1D_1}}{S_{AB_1CD_1}} = \sqrt{3}\).