
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 278 Атанасян — Подробные Ответы
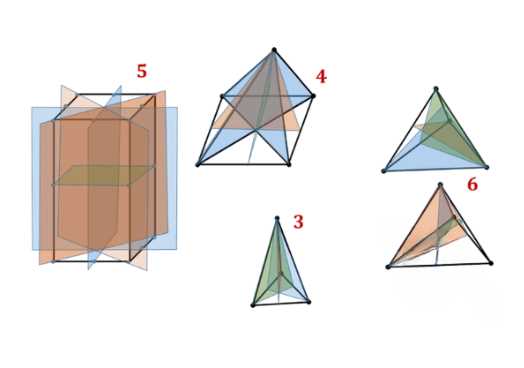
Сколько плоскостей симметрии имеет:
а) правильная четырёхугольная призма, отличная от куба;
б) правильная четырёхугольная пирамида;
в) правильная треугольная пирамида?
а) правильная четырехугольная призма, не куб: плоскости симметрии проходят через середины противоположных боковых граней и диагонали оснований. Ответ: \(5\).
б) правильная четырехугольная пирамида: плоскости симметрии проходят через вершину и диагонали основания. Ответ: \(4\).
в) правильная треугольная пирамида: если не все ребра равны, плоскости симметрии проходят через вершину и высоту основания. Ответ: \(3\). Если все ребра равны, добавляются плоскости через ребро и середину противоположной стороны. Ответ: \(6\).
Ответ: а) \(5\); б) \(4\); в) \(3\) и \(6\).
Рассмотрим подробное объяснение количества плоскостей симметрии для каждой фигуры.
Для правильной четырехугольной призмы, которая не является кубом, плоскости симметрии включают вертикальные плоскости, проходящие через середины противоположных боковых граней. Таких плоскостей три. Дополнительно есть две плоскости, проходящие через диагонали верхнего и нижнего оснований. В сумме получается пять плоскостей симметрии.
В случае правильной четырехугольной пирамиды с квадратным основанием плоскости симметрии проходят через вершину и диагонали основания, что дает две плоскости. Еще две плоскости проходят через вершину и середины противоположных сторон основания. Таким образом, общее количество плоскостей симметрии равно четырем.
Для правильной треугольной пирамиды ситуация зависит от равенства ребер. Если не все ребра равны, то плоскости симметрии проходят только через вершину и высоты основания, их количество равно трем. Если же пирамида является правильным тетраэдром, то добавляются дополнительные плоскости симметрии, проходящие через ребро и середину противоположной стороны. В этом случае общее количество плоскостей увеличивается до шести.
Итоговые ответы: для призмы — пять плоскостей, для четырехугольной пирамиды — четыре, для треугольной пирамиды — три или шесть в зависимости от равенства ребер.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!