
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 277 Атанасян — Подробные Ответы
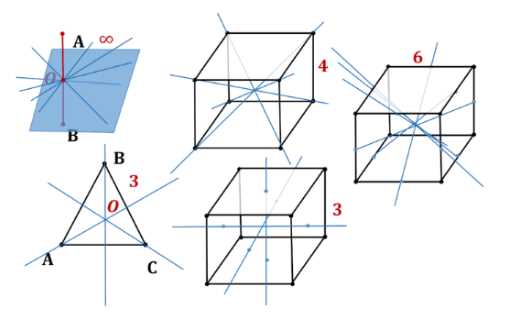
Сколько осей симметрии имеет:
а) отрезок;
б) правильный треугольник;
в) куб?
а) отрезок имеет \(\infty\) осей симметрии (все прямые, перпендикулярные ему и проходящие через его середину).
б) правильный треугольник имеет три оси симметрии (каждая проходит через вершину и середину противоположной стороны).
в) куб имеет 13 осей симметрии:
— 4 проходят через противоположные вершины,
— 3 через центры противоположных граней,
— 6 через середины противоположных рёбер.
Рассмотрим пошаговое рассуждение для определения количества осей симметрии каждой фигуры.
Для отрезка: ось симметрии — это прямая, при отражении относительно которой фигура совмещается сама с собой. Любая прямая, перпендикулярная отрезку и проходящая через его середину, будет осью симметрии. Поскольку таких прямых можно провести бесконечно много (под любым углом в перпендикулярной плоскости), то отрезок имеет \(( \infty )\) осей симметрии.
Для правильного треугольника: ось симметрии должна делить фигуру на две зеркально равные части. В правильном треугольнике каждая ось проходит через вершину и середину противоположной стороны. Так как вершин три, то и осей симметрии три.
Для куба: здесь требуется более детальный анализ. Оси симметрии куба делятся на три типа:
1) Оси, проходящие через противоположные вершины: таких диагоналей у куба 4, каждая задаёт ось симметрии третьего порядка (поворот на \(( 120^\circ )\) вокруг неё сохраняет куб).
2) Оси, проходящие через центры противоположных граней: их 3, соответствуют осям симметрии четвёртого порядка (поворот на \(( 90^\circ )\)).
3) Оси, проходящие через середины противоположных рёбер: их 6, задают оси симметрии второго порядка (поворот на \(( 180^\circ )\)).
Суммируя: \(( 4 + 3 + 6 = 13 )\) осей симметрии. Каждый тип осей соответствует определённому преобразованию симметрии, сохраняющему куб.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!