
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 276 Атанасян — Подробные Ответы
Сколько центров симметрии имеет:
а) параллелепипед;
б) правильная треугольная призма;
в) двугранный угол;
г) отрезок?
Решение:
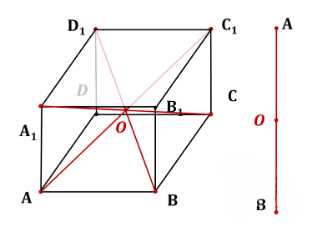
а) параллелепипед имеет один центр симметрии \(O\), который является точкой пересечения его диагоналей.
б) правильная треугольная призма не имеет центра симметрии.
в) двугранный угол не имеет центра симметрии.
г) отрезок имеет один центр симметрии \(O\), который является его серединой.
Ответ: а) один; б) нет; в) нет; г) один.
Рассмотрим пошаговое рассуждение для определения центров симметрии каждой фигуры. Начнем с параллелепипеда. Центр симметрии — это точка, относительно которой любая точка фигуры имеет симметричную ей точку, также принадлежащую фигуре. В параллелепипеде такой точкой является пересечение его диагоналей. Если провести диагонали \(A_1C\) и \(AC_1\), они пересекутся в точке \(O\), которая и будет центром симметрии. Для любой вершины, например \(A\), симметричная ей вершина \(A_1\) будет лежать на противоположной стороне параллелепипеда, а отрезок \(AA_1\) пройдет через \(O\).
Перейдем к правильной треугольной призме. Эта фигура состоит из двух равных правильных треугольников, расположенных параллельно, и трех прямоугольников, соединяющих их стороны. Проверим наличие центра симметрии. Если бы он существовал, то для каждой вершины нижнего треугольника, например \(A\), должна найтись симметричная вершина \(A’\) в верхнем треугольнике, такая что середина отрезка \(AA’\) совпадает с центром симметрии. Однако в правильной треугольной призме вершины верхнего и нижнего треугольников не расположены друг напротив друга из-за их смещения на \(120^\circ\). Поэтому такой точки \(O\) не существует, и призма не имеет центра симметрии.
Теперь рассмотрим двугранный угол, который образован двумя полуплоскостями, пересекающимися по прямой. Предположим, что у него есть центр симметрии \(O\). Тогда для любой точки \(P\) на одной грани должна найтись симметричная точка \(P’\) на другой грани, такая что \(O\) — середина отрезка \(PP’\). Однако двугранный угол бесконечен в направлении, перпендикулярном его ребру, и не имеет ограниченной фигуры, для которой можно было бы определить такую точку. Следовательно, он не обладает центром симметрии.
Наконец, возьмем отрезок \(AB\). Его центром симметрии является середина \(O\), так как для любой точки \(P\) на отрезке существует симметричная точка \(P’\), такая что \(O\) делит \(PP’\) пополам. Например, если \(P\) находится на расстоянии \(x\) от \(A\), то \(P’\) будет на расстоянии \(x\) от \(B\), и \(O\) останется серединой. Таким образом, отрезок имеет ровно один центр симметрии.
Итоговый вывод: параллелепипед и отрезок обладают одним центром симметрии, а правильная треугольная призма и двугранный угол не имеют центров симметрии. Ответы соответствуют приведенному примеру: а) один; б) нет; в) нет; г) один.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!