
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 275 Атанасян — Подробные Ответы
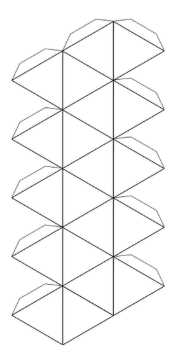
Перерисуйте развёртку правильного икосаэдра на плотный лист бумаги в большем масштабе, вырежьте развёртку и склейте из неё икосаэдр.
Развёртка правильного икосаэдра состоит из 20 равносторонних треугольников. Для построения:
Вычисли длину стороны \(a\) по формуле площади правильного треугольника \(S = \frac{\sqrt{3}}{4} \cdot a^2\). Увеличь масштаб, сохраняя пропорции. Вырежи развёртку по контуру, оставив клапаны для склеивания. Согни по линиям и склей грани, формируя икосаэдр. Объём получившегося икосаэдра можно вычислить по формуле \(V = \frac{5}{12} \cdot (3 + \sqrt{5}) \cdot a^3\).
Для решения задачи о склеивании правильного икосаэдра из развёртки необходимо выполнить следующие шаги. Сначала убедитесь, что развёртка содержит 20 равносторонних треугольников, так как икосаэдр состоит из 20 граней. Каждый треугольник должен иметь одинаковую длину стороны \(a\), чтобы все грани были конгруэнтными.
Далее, для построения развёртки в увеличенном масштабе, рассчитайте длину стороны \(a\) исходя из желаемого размера икосаэдра. Площадь одного равностороннего треугольника вычисляется по формуле \(S = \frac{\sqrt{3}}{4} \cdot a^2\). Умножьте все линейные размеры развёртки на коэффициент масштабирования, сохраняя пропорции.
После увеличения масштаба аккуратно вырежьте развёртку по контуру, оставляя небольшие клапаны по краям треугольников для склеивания. Клапаны должны быть достаточно широкими, чтобы обеспечить прочное соединение граней.
Затем согните развёртку по линиям между треугольниками, формируя трёхмерную структуру. Угол между двумя соседними гранями икосаэдра равен \(\arccos\left(-\frac{\sqrt{5}}{3}\right)\), что примерно составляет \(138.19^\circ\). Это поможет правильно ориентировать грани при склеивании.
Начинайте склеивать грани, соединяя клапаны соседних треугольников. Рекомендуется сначала собрать пять треугольников вокруг одной вершины, образуя пятиугольную пирамиду, а затем постепенно добавлять остальные грани, следуя схеме развёртки.
После завершения склеивания проверьте, что все рёбра икосаэдра имеют одинаковую длину, а все двугранные углы соответствуют теоретическому значению. Объём получившегося икосаэдра можно вычислить по формуле \(V = \frac{5}{12} \cdot (3 + \sqrt{5}) \cdot a^3\), где \(a\) — длина ребра.
Для проверки правильности сборки убедитесь, что в каждой вершине сходятся пять рёбер, а общее количество вершин равно 12, что соответствует свойствам правильного икосаэдра. Если все шаги выполнены корректно, у вас получится точная модель правильного икосаэдра.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!