
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 274 Атанасян — Подробные Ответы
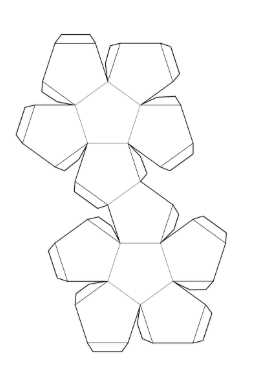
Перерисуйте развёртку правильного додекаэдра на плотный лист бумаги в большем масштабе, вырежьте развёртку и склейте из неё додекаэдр.
Развёртка правильного додекаэдра состоит из 12 правильных пятиугольников. Площадь каждого пятиугольника можно вычислить по формуле \(S = \frac{5}{4} \cdot a^2 \cdot \cot\left(\frac{\pi}{5}\right)\), где \(a\) — длина стороны. Угол между соседними гранями при склеивании равен \(\frac{2\pi}{5}\). Для построения развёртки начертите центральный пятиугольник и пристройте к каждой его стороне ещё по пятиугольнику. Вырежьте развёртку и аккуратно склейте рёбра, совмещая соответствующие стороны. Объём получившегося додекаэдра вычисляется по формуле \(V = \frac{15 + 7\sqrt{5}}{4} \cdot a^3\).
Построение развёртки правильного додекаэдра требует последовательного геометрического анализа. Начнём с того, что додекаэдр состоит из 12 правильных пятиугольников, каждый из которых имеет одинаковые стороны и углы. Для вычисления параметров пятиугольника используем формулу площади \((S = \frac{5}{4} \cdot a^2 \cdot \cot(\frac{\pi}{5}))\), где \(a\) — длина стороны. Угол между двумя соседними гранями в трёхмерном пространстве составляет \((\frac{2\pi}{5})\).
Следующий шаг — построение центрального пятиугольника на бумаге. Это будет основа развёртки. Затем к каждой стороне центрального пятиугольника нужно достроить ещё по одному пятиугольнику. Важно соблюдать точность углов и длин сторон, чтобы при склеивании все рёбра совпали. Для проверки правильности развёртки можно использовать свойство додекаэдра: сумма плоских углов при каждой вершине должна быть меньше \((2\pi)\), конкретно \((\frac{3\pi}{5})\) для каждой вершины.
После вырезания развёртки аккуратно согните её по линиям, соответствующим рёбрам додекаэдра. Склейте соседние грани, начиная с центрального пятиугольника и постепенно двигаясь к краям. Убедитесь, что все рёбра плотно прилегают друг к другу, иначе форма будет деформирована. Объём готового додекаэдра можно проверить по формуле \((V = \frac{15 + 7\sqrt{5}}{4} \cdot a^3)\). Если все шаги выполнены правильно, у вас получится идеальный правильный додекаэдр.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!