ГДЗ по Геометрии 10 класс Номер 273 Атанасян — Подробные Ответы

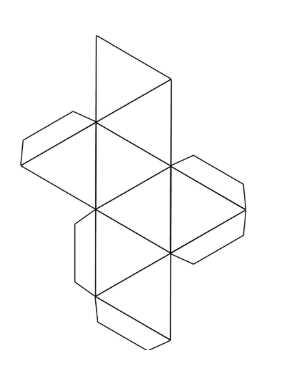
Перерисуйте развёртку правильного октаэдра на плотный лист бумаги в большем масштабе, вырежьте развёртку и склейте из неё октаэдр.

Развёртка правильного октаэдра состоит из 8 равносторонних треугольников. Для склеивания октаэдра: перерисуйте развёртку на плотную бумагу, увеличьте масштаб, вырежьте по контуру, согните по линиям сгиба и склейте грани. Объём октаэдра с ребром \(a\) вычисляется по формуле \(V = \frac{\sqrt{2}}{3} \cdot a^3\). Площадь поверхности \(S = 2 \cdot \sqrt{3} \cdot a^2\).

Для решения задачи о склеивании правильного октаэдра из развёртки необходимо выполнить несколько шагов. Сначала нужно понять, что правильный октаэдр — это многогранник, состоящий из восьми равносторонних треугольников, соединённых таким образом, что в каждой вершине сходятся четыре ребра. Развёртка октаэдра представляет собой плоскую фигуру, которую можно сложить в трёхмерный объект.

Развёртка правильного октаэдра обычно имеет форму креста, состоящего из восьми треугольников. Каждый треугольник имеет сторону \(a\), и все углы равны \(60^\circ\). Площадь одного треугольника вычисляется по формуле \(S_{\triangle} = \frac{\sqrt{3}}{4} \cdot a^2\), а общая площадь поверхности октаэдра равна \(S = 8 \cdot S_{\triangle} = 2 \cdot \sqrt{3} \cdot a^2\).

Чтобы склеить октаэдр, нужно аккуратно перерисовать развёртку на плотной бумаге, соблюдая размеры. Затем вырезать её по контуру, оставив небольшие клапаны для склеивания. После этого согнуть развёртку по линиям сгиба так, чтобы треугольники соединились в вершинах. Склеивать следует последовательно, начиная с центральных граней, чтобы конструкция была устойчивой.

Объём получившегося октаэдра можно вычислить по формуле \(V = \frac{\sqrt{2}}{3} \cdot a^3\). Важно следить за тем, чтобы все рёбра были одинаковой длины, а углы между гранями соответствовали \(109.5^\circ\) — это характерный угол для правильного октаэдра. Если развёртка нарисована правильно, а склеивание выполнено аккуратно, получится идеальный правильный октаэдр.