Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 272 Атанасян — Подробные Ответы
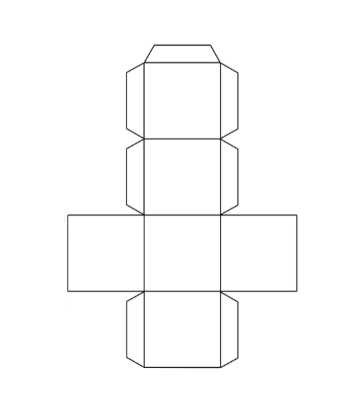
Перерисуйте развёртку куба на плотный лист бумаги в большем масштабе, вырежьте развёртку и склейте из неё куб.
Развёртка правильного куба состоит из 6 квадратов, соединённых сторонами. Площадь поверхности куба \(S = 6a^2\), где \(a\) — длина ребра. Объём куба \(V = a^3\). Для склеивания куба из развёртки необходимо аккуратно согнуть её по линиям соединения квадратов и склеить соответствующие грани.
Для решения задачи о склеивании куба из его развёртки необходимо выполнить следующие шаги. Сначала нужно убедиться, что развёртка действительно соответствует правильному кубу, то есть состоит из шести квадратов, соединённых таким образом, что при складывании они образуют замкнутую фигуру. Площадь поверхности куба вычисляется по формуле \(S = 6a^2\), где \(a\) — длина ребра куба. Объём куба определяется как \(V = a^3\).
Далее следует перенести развёртку на плотную бумагу, увеличив её масштаб для удобства работы. Важно сохранить пропорции всех квадратов и их взаимное расположение. После вырезания развёртки по контуру необходимо аккуратно согнуть её по линиям соединения квадратов. Эти линии должны быть чёткими, чтобы сгибы получились ровными.
При склеивании куба важно последовательно соединять соответствующие грани. Обычно для этого оставляют небольшие клапаны на краях развёртки, которые затем намазывают клеем и прижимают к соседним граням. После склеивания всех сторон куб должен получиться ровным, без перекосов. Если развёртка составлена правильно, все рёбра куба будут одинаковой длины, а углы — прямыми.
В процессе работы можно проверить правильность сборки, убедившись, что каждая грань куба является квадратом со стороной \(a\), а все рёбра сходятся в вершинах под прямыми углами. Если развёртка была выполнена без ошибок, итоговый куб будет соответствовать заданным параметрам.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.