ГДЗ по Геометрии 10 класс Номер 271 Атанасян — Подробные Ответы

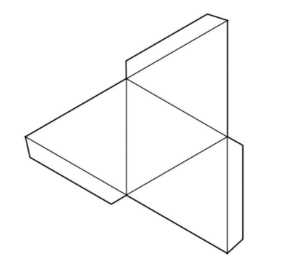
Перерисуйте развёртку правильного тетраэдра на плотный лист бумаги в большем масштабе, вырежьте развёртку (сделав необходимые припуски для склеивания) и склейте из неё тетраэдр.

Развёртка правильного тетраэдра состоит из четырёх равносторонних треугольников. Для склеивания:

1. Перерисуйте развёртку в большем масштабе, сохраняя углы \(60^\circ\) и равные стороны \(a\).
2. Добавьте припуски для склеивания вдоль одного ребра каждого треугольника.
3. Вырежьте развёртку по контуру.
4. Согните по рёбрам и склейте припуски, формируя тетраэдр.

Объём получившегося тетраэдра: \(V = \frac{a^3}{6\sqrt{2}}\).

Чтобы объяснить процесс склеивания правильного тетраэдра из его развёртки максимально подробно, начнём с понимания самой развёртки. Развёртка правильного тетраэдра представляет собой плоскую фигуру, состоящую из четырёх равносторонних треугольников, соединённых между собой рёбрами. Каждый треугольник имеет одинаковые стороны длиной \(a\) и углы \(60^\circ\).

Первым шагом необходимо аккуратно перерисовать развёртку на плотную бумагу или картон, увеличив масштаб для удобства работы. Важно сохранить точные геометрические пропорции: все стороны должны быть равны \(a\), а углы строго \(60^\circ\). Если развёртка нарисована от руки, можно воспользоваться линейкой и транспортиром для проверки точности.

Далее нужно добавить припуски для склеивания. Припуски — это небольшие полоски бумаги, которые будут накладываться на соседние грани при сборке. Обычно их делают шириной около \(5-10\) мм вдоль одного ребра каждого треугольника. Например, если у вас четыре треугольника в развёртке, то припуски добавляются к трём из них (так как одна грань останется свободной).

После этого развёртку вырезают по внешнему контуру, включая припуски. Ножницы должны двигаться плавно, чтобы края были ровными — это важно для качественной склейки. Если бумага слишком тонкая, можно укрепить её, наклеив на картон перед вырезанием.

Теперь можно приступать к сборке. Сначала согните развёртку по всем намеченным рёбрам. Лучше делать это последовательно, начиная с центрального треугольника и постепенно присоединяя соседние грани. Чтобы сгибы были чёткими, можно провести по ним тупой стороной ножниц или специальным инструментом для биговки.

Затем нанесите клей на припуски и аккуратно соедините грани. Удобнее всего использовать клей-карандаш или ПВА, так как они не деформируют бумагу. Прижмите склеиваемые поверхности на несколько секунд, чтобы соединение стало прочным. Важно следить, чтобы все рёбра тетраэдра сошлись в одной вершине без перекосов.

После склейки дайте модели высохнуть. Если где-то остались щели или неровности, их можно дополнительно проклеить тонкими полосками бумаги. Готовый тетраэдр должен иметь все рёбра равной длины \(a\) и все грани — равносторонние треугольники.

Объём получившегося тетраэдра вычисляется по формуле \(V = \frac{a^3}{6\sqrt{2}}\). Эта формула следует из того, что высота правильного тетраэдра \(h\) связана с длиной ребра соотношением \(h = a \sqrt{\frac{2}{3}}\), а площадь основания (равностороннего треугольника) равна \(S = \frac{a^2 \sqrt{3}}{4}\). Подставляя эти значения в формулу объёма пирамиды \(V = \frac{1}{3} S h\), получаем искомый результат.

Для проверки правильности сборки можно измерить все рёбра и углы: если тетраэдр действительно правильный, все двугранные углы между гранями будут равны \(\arccos\left(\frac{1}{3}\right)\), а каждая вершина будет соединена с тремя другими рёбрами одинаковой длины. Если обнаружены перекосы, их можно исправить, аккуратно подрезав или доклеив припуски.

Таким образом, процесс склеивания тетраэдра требует внимательности на каждом этапе: от точного построения развёртки до аккуратной сборки. Если всё сделано правильно, получится идеальная геометрическая фигура, демонстрирующая свойства правильного многогранника.