
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 270 Атанасян — Подробные Ответы
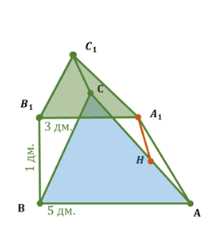
Основаниями усечённой пирамиды являются правильные треугольники со сторонами 5 см и 3 см соответственно. Одно из боковых рёбер пирамиды перпендикулярно к плоскостям оснований и равно 1 см. Найдите площадь боковой поверхности усечённой пирамиды.
По условию \(ABCA_1B_1C_1\) — усечённая пирамида. \(BB_1 = CC_1 \Rightarrow\) трапеция \(B_1C_1CB\) — равнобедренная. \(AM \perp BC\), \(A_1M_1 \perp B_1C_1 \Rightarrow M_1M \parallel BC\), по теореме (о трёх перпендикулярах) \(MM_1\) — высота боковой грани. \(M_1O \perp AM\).
Из \(\triangle A_1M_1B_1\) по определению синуса:
\(A_1M_1 = A_1B_1 \cdot \sin 60^\circ = 3\sqrt{3} \, \text{см}.\)
Из \(\triangle AMB\) аналогично:
\(AM = AB \cdot \sin 60^\circ = 5\sqrt{3} \, \text{см}.\)
\(OM = AM — AO = AM — A_1M_1 = 5\sqrt{3} — 3\sqrt{3} = 2\sqrt{3} \, \text{см}.\)
Из \(\triangle M_1OM\): \(\angle M_1OM = 90^\circ\), по теореме Пифагора:
\(MM_1 = \sqrt{M_1O^2 + OM^2} = \sqrt{1^2 + (\sqrt{3})^2} = 2 \, \text{см}.\)
Площадь боковой грани \(B_1C_1CB\):
\(S_{B_1C_1CB} = \frac{B_1C_1 + BC}{2} \cdot MM_1 = \frac{3 + 5}{2} \cdot 2 = 8 \, \text{см}^2.\)
Площади боковых граней \(AA_1C_1C\) и \(AA_1B_1B\):
\(S_{AA_1C_1C} = S_{AA_1B_1B} = \frac{3 + 5}{2} \cdot 1 = 4 \, \text{см}^2.\)
Общая площадь боковой поверхности:
\(S_{\text{бок}} = S_{B_1C_1CB} + S_{AA_1B_1B} + S_{AA_1C_1C} = 8 + 4 + 4 = 16 \, \text{см}^2.\)
Рассмотрим решение задачи об усечённой пирамиде \(ABCA_1B_1C_1\) максимально подробно.
Исходные данные: усечённая пирамида с основаниями \(ABC\) (нижнее) и \(A_1B_1C_1\) (верхнее), причём \(BB_1 = CC_1\). Это означает, что боковая грань \(B_1C_1CB\) является равнобедренной трапецией.
Для решения проводим вспомогательные построения. Из точек \(A\) и \(A_1\) опускаем перпендикуляры \(AM\) и \(A_1M_1\) на стороны \(BC\) и \(B_1C_1\) соответственно. По свойствам усечённой пирамиды, отрезок \(MM_1\), соединяющий основания этих перпендикуляров, будет параллелен \(BC\) и одновременно являться высотой боковой грани \(B_1C_1CB\). Это следует из теоремы о трёх перпендикулярах, так как \(M_1O\) перпендикулярен \(AM\).
Переходим к вычислениям. В треугольнике \(A_1M_1B_1\) с углом \(60^\circ\) находим длину \(A_1M_1\) через синус: \(A_1M_1 = A_1B_1 \cdot \sin(60^\circ) = 3\sqrt{3}\) см. Аналогично для треугольника \(AMB\) получаем \(AM = AB \cdot \sin(60^\circ) = 5\sqrt{3}\) см. Разность этих величин даёт нам длину отрезка \(OM = AM — A_1M_1 = 2\sqrt{3}\) см.
Теперь определяем высоту боковой грани \(MM_1\). Рассматриваем прямоугольный треугольник \(M_1OM\), где по теореме Пифагора: \(MM_1 = \sqrt{M_1O^2 + OM^2} = \sqrt{1 + 3} = 2\) см.
Вычисляем площади боковых граней. Для трапеции \(B_1C_1CB\) площадь равна \(S = \frac{B_1C_1 + BC}{2} \cdot MM_1 = \frac{3 + 5}{2} \cdot 2 = 8\) см². Две другие боковые грани \(AA_1B_1B\) и \(AA_1C_1C\) имеют одинаковую площадь: \(S = \frac{3 + 5}{2} \cdot 1 = 4\) см² каждая.
Итоговая площадь боковой поверхности складывается из площадей всех трёх граней: \(S_{бок} = 8 + 4 + 4 = 16\) см².
В ходе решения последовательно использовались свойства усечённой пирамиды, тригонометрические соотношения в прямоугольных треугольниках и формула площади трапеции. Каждый шаг логически вытекает из предыдущего, что обеспечивает корректность конечного результата.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!