ГДЗ по Геометрии 10 класс Номер 269 Атанасян — Подробные Ответы

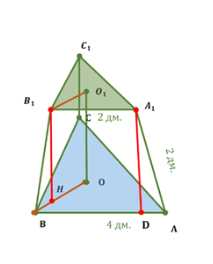
Стороны оснований правильной треугольной усечённой пирамиды равны 4 дм и 2 дм, а боковое ребро равно 2 дм. Найдите высоту и апофему пирамиды.

Дано усечённая правильная пирамида \(ABCA_1B_1C_1\) с основаниями \(ABC\) и \(A_1B_1C_1\), где \(A_1A = 2\) дм, \(AB = 4\) дм, \(A_1B_1 = 2\) дм. Найдём высоту и апофему пирамиды.

Апофема \(A_1D\) находится как высота равнобедренной трапеции \(AA_1B_1B\):
\(
A_1D = \sqrt{A_1A^2 — \left(\frac{AB — A_1B_1}{2}\right)^2} = \sqrt{4 — 1} = \sqrt{3} \text{ дм}
\)

Высота пирамиды \(B_1H\) находится через радиусы описанных окружностей оснований:
\(
R_{ABC} = \frac{AB}{\sqrt{3}} = \frac{4\sqrt{3}}{3} \text{ дм}, \quad R_{A_1B_1C_1} = \frac{A_1B_1}{\sqrt{3}} = \frac{2\sqrt{3}}{3} \text{ дм}
\)
\(
B_1H = \sqrt{B_1B^2 — (R_{ABC} — R_{A_1B_1C_1})^2} = \sqrt{4 — \left(\frac{2\sqrt{3}}{3}\right)^2} = \sqrt{4 — \frac{4}{3}} = \sqrt{\frac{8}{3}} = \)
\(=\frac{2\sqrt{6}}{3} \text{ дм}
\)

Ответ: \(\sqrt{3}\) дм, \(\frac{2\sqrt{6}}{3}\) дм.

Рассмотрим усечённую правильную треугольную пирамиду \(ABCA_1B_1C_1\) с нижним основанием \(ABC\) и верхним основанием \(A_1B_1C_1\), параллельным нижнему. Центры оснований обозначим как \(O\) и \(O_1\) соответственно. Дано: \(A_1A = 2\) дм (боковое ребро), \(AB = 4\) дм (сторона нижнего основания), \(A_1B_1 = 2\) дм (сторона верхнего основания).

Для нахождения апофемы рассмотрим боковую грань \(AA_1B_1B\), которая является равнобедренной трапецией. Апофема усечённой пирамиды — это высота этой трапеции. Обозначим её как \(A_1D\). Проведём перпендикуляр \(A_1D\) из точки \(A_1\) на сторону \(AB\). Длина отрезка \(DA\) равна полуразности сторон оснований:
\(
DA = \frac{AB — A_1B_1}{2} = \frac{4 — 2}{2} = 1 \text{ дм}
\)
Применяя теорему Пифагора к прямоугольному треугольнику \(AA_1D\), получаем:
\(
A_1D = \sqrt{A_1A^2 — DA^2} = \sqrt{2^2 — 1^2} = \sqrt{4 — 1} = \sqrt{3} \text{ дм}
\)

Для нахождения высоты пирамиды \(H\) рассмотрим разность радиусов описанных окружностей оснований. Для правильного треугольника радиус описанной окружности вычисляется по формуле:
\(
R = \frac{a}{\sqrt{3}}
\)
Таким образом:
\(
R_{ABC} = \frac{AB}{\sqrt{3}} = \frac{4\sqrt{3}}{3} \text{ дм}, \quad R_{A_1B_1C_1} = \frac{A_1B_1}{\sqrt{3}} = \frac{2\sqrt{3}}{3} \text{ дм}
\)
Разность радиусов:
\(
\Delta R = R_{ABC} — R_{A_1B_1C_1} = \frac{4\sqrt{3}}{3} — \frac{2\sqrt{3}}{3} = \frac{2\sqrt{3}}{3} \text{ дм}
\)
Высота пирамиды \(H\) является катетом прямоугольного треугольника, образованного боковым ребром \(B_1B\) и разностью радиусов \(\Delta R\). По теореме Пифагора:
\(
H = \sqrt{B_1B^2 — (\Delta R)^2} = \sqrt{2^2 — \left(\frac{2\sqrt{3}}{3}\right)^2} = \sqrt{4 — \frac{12}{9}} = \sqrt{4 — \frac{4}{3}} = \sqrt{\frac{8}{3}} = \)
\(=\frac{2\sqrt{6}}{3} \text{ дм}
\)

Ответ: апофема равна \(\sqrt{3}\) дм, высота пирамиды равна \(\frac{2\sqrt{6}}{3}\) дм.