Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 268 Атанасян — Подробные Ответы
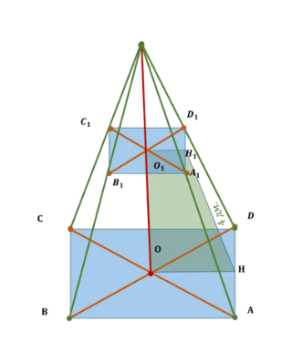
Плоскость, параллельная плоскости основания правильной четырёхугольной пирамиды, делит высоту пирамиды в отношении \(1 : 2\), считая от вершины пирамиды. Апофема полученной усечённой пирамиды равна 4 дм, а площадь её полной поверхности равна \(186 \, \text{дм}^2\). Найдите высоту усечённой пирамиды.
Дано: \(ABCDK\) — пирамида, \(K\) — вершина, \(KO \perp ABCDEF\), \(A_1B_1C_1D_1 \parallel ABCD\), \(O_1 \in A_1B_1C_1D_1\), \(KO_1 \perp O_1O\), \(H_1H = 4\) дм., апофема \(S_{ABCDA_1B_1C_1D_1} = 186\) дм\(^2\). Найти: \(O_1O\).
Решение: Обозначим сторону меньшего основания \(A_1B_1 = x\). Тогда \(AB = 3x\). Площадь усечённой пирамиды: \[S_{ABCDA_1B_1C_1D_1} = 9x^2 + x^2 + 4 \cdot 2x^2 = 186\] \[10x^2 + 32x — 186 = 0\] Дискриминант: \[D = 16^2 + 1860 = 2116 = 46^2\] Корень: \[x = \frac{-16 + 46}{10} = 3 \text{ дм}\] Тогда \(AB = 9\) дм. По теореме Пифагора: \[O_1O = \sqrt{H_1H^2 — \left(\frac{AB — A_1B_1}{2}\right)^2} = \sqrt{16 — 9} = \sqrt{7} \text{ дм}\] Ответ: \(O_1O = \sqrt{7}\) дм.
Дано: \(ABCDK\) — правильная четырёхугольная пирамида с вершиной \(K\), \(KO\) — высота пирамиды, перпендикулярная плоскости основания \(ABCD\), \(A_1B_1C_1D_1\) — сечение, параллельное основанию, \(O_1\) — центр сечения, \(KO_1\) — высота усечённой пирамиды, перпендикулярная отрезку \(O_1O\), \(H_1H = 4\) дм — апофема боковой грани усечённой пирамиды, \(S_{ABCDA_1B_1C_1D_1} = 186\) дм\(^2\) — площадь полной поверхности усечённой пирамиды. Требуется найти длину отрезка \(O_1O\).
Рассуждение решения:
1. Обозначим сторону меньшего основания \(A_1B_1C_1D_1\) через \(x\). Поскольку \(A_1B_1C_1D_1 \parallel ABCD\) и пирамида правильная, то стороны подобны, и можно записать соотношение сторон: \(AB = k \cdot x\), где \(k\) — коэффициент подобия. Из условия задачи следует, что \(AB = 3x\), так как площадь полной поверхности усечённой пирамиды выражается через \(x\) и \(3x\).
2. Площадь полной поверхности усечённой пирамиды складывается из площадей двух оснований и четырёх боковых граней: \[S_{ABCDA_1B_1C_1D_1} = S_{ABCD} + S_{A_1B_1C_1D_1} + 4 \cdot S_{AA_1D_1D}\] Для правильной четырёхугольной пирамиды площади оснований равны квадрату стороны: \[S_{ABCD} = (3x)^2 = 9x^2\] \[S_{A_1B_1C_1D_1} = x^2\] Боковая грань \(AA_1D_1D\) — трапеция, её площадь можно выразить как: \[S_{AA_1D_1D} = \frac{AB + A_1B_1}{2} \cdot H_1H = \frac{3x + x}{2} \cdot 4 = 8x\] Таким образом, полная площадь: \[9x^2 + x^2 + 4 \cdot 8x = 10x^2 + 32x = 186\]
3. Получаем квадратное уравнение: \[10x^2 + 32x — 186 = 0\] Упростим его, разделив на 2: \[5x^2 + 16x — 93 = 0\] Дискриминант: \[D = 16^2 — 4 \cdot 5 \cdot (-93) = 256 + 1860 = 2116\] Корень из дискриминанта: \[\sqrt{D} = 46\] Находим корни уравнения: \[x = \frac{-16 \pm 46}{10}\] Поскольку длина стороны положительна, берём положительный корень: \[x = \frac{-16 + 46}{10} = \frac{30}{10} = 3 \text{ дм}\] Таким образом, \(A_1B_1 = 3\) дм, \(AB = 9\) дм.
4. Для нахождения \(O_1O\) рассмотрим прямоугольный треугольник, образованный высотой усечённой пирамиды \(H_1H\), отрезком \(O_1O\) и половиной разности сторон оснований. Разность сторон: \[AB — A_1B_1 = 9 — 3 = 6 \text{ дм}\] Половина разности: \[\frac{6}{2} = 3 \text{ дм}\] По теореме Пифагора: \[O_1O = \sqrt{H_1H^2 — 3^2} = \sqrt{16 — 9} = \sqrt{7} \text{ дм}\]
Ответ: \(O_1O = \sqrt{7}\) дм.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.