ГДЗ по Геометрии 10 класс Номер 267 Атанасян — Подробные Ответы

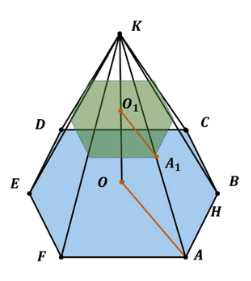
Пирамида пересечена плоскостью, параллельной основанию. Докажите, что боковые рёбра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Рассмотрим плоскость \(AOK\), проходящую через высоту \(KO\) и ребро \(AK\). По условию \(a \parallel ABCDEF\) и \(O_1A_1 \subset a\), \(OA \subset ABCDEF\), следовательно, \(O_1A_1 \parallel OA\). По расширенной теореме Фалеса в плоскости \(AOK\) отрезки \(AK\) и \(KO\) делятся плоскостью \(a\) на пропорциональные части. Аналогично для остальных рёбер. Таким образом, боковые рёбра и высота пирамиды делятся плоскостью \(a\) на пропорциональные части. Что и требовалось доказать.

Рассмотрим задачу о пирамиде \(ABCDEFK\) с вершиной \(K\), где \(KO\) — высота, перпендикулярная основанию \(ABCDEF\), и дана плоскость \(a\), параллельная основанию. Требуется доказать, что боковые рёбра и высота пирамиды делятся плоскостью \(a\) на пропорциональные части.

Шаг 1. Построение плоскости \(AOK\). Выберем одно из боковых рёбер, например \(AK\), и проведём плоскость через это ребро и высоту \(KO\). Эта плоскость будет содержать треугольник \(AOK\), где \(O\) — точка пересечения высоты с основанием.

Шаг 2. Анализ параллельности. По условию плоскость \(a\) параллельна основанию \(ABCDEF\), значит, любая прямая, лежащая в \(a\), параллельна соответствующей прямой в основании. В частности, отрезок \(O_1A_1\), принадлежащий плоскости \(a\), параллелен отрезку \(OA\) из основания.

Шаг 3. Применение теоремы Фалеса. В плоскости \(AOK\) прямые \(O_1A_1\) и \(OA\) параллельны, поэтому по расширенной теореме Фалеса секущая плоскость \(a\) делит стороны \(AK\) и \(KO\) пропорционально. То есть, если плоскость \(a\) пересекает \(AK\) в точке \(A_1\), а \(KO\) в точке \(O_1\), то выполняется соотношение:
\[
\frac{KA_1}{A_1A} = \frac{KO_1}{O_1O}
\]

Шаг 4. Обобщение на все рёбра. Аналогичные рассуждения можно провести для любого другого бокового ребра, например \(BK\), \(CK\) и т. д. В каждом случае плоскость \(a\) будет пересекать ребро и высоту, сохраняя пропорциональность деления.

Шаг 5. Вывод. Таким образом, плоскость \(a\), параллельная основанию, делит все боковые рёбра и высоту пирамиды в одинаковом соотношении, что и требовалось доказать. Это свойство является частным случаем общего принципа сечения пирамиды параллельной плоскостью.