Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 266 Атанасян — Подробные Ответы
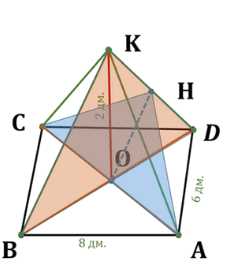
Основанием пирамиды, высота которой равна 2 дм, а боковые рёбра равны друг другу, является прямоугольник со сторонами 6 дм и 8 дм. Найдите площадь сечения, проведённого через диагональ основания параллельно боковому ребру.
Дано: пирамида \(ABCDK\), где \(ABCD\) — прямоугольник с \(AB = 8\) дм, \(BC = 6\) дм. \(KO \perp ABCD\), \(KA = KB = KC = KD = \sqrt{29}\) дм, \(KO = 2\) дм. \(ACH \parallel BK\).
Найти: \(S_{CHA}\).
Решение:
По теореме Пифагора в \(\triangle ABD\):
\(BD^2 = AB^2 + AD^2 = 64 + 36 = 100 \Rightarrow BD = 10 \text{ дм}.\)
Так как \(KA = KB = KC = KD\), точка \(O\) — центр прямоугольника, поэтому \(BO = \frac{BD}{2} = 5\) дм.
В плоскости \(BKD\):
Так как \(ACH \parallel BK\) и \(OH \subset ACH\), то \(OH \parallel BK\).
Из подобия \(\triangle KDB\) и \(\triangle KHO\):
\(\frac{HO}{DB} = \frac{KO}{KB} \Rightarrow HO = \frac{KO \cdot DB}{KB} = \frac{2 \cdot 10}{\sqrt{29}} = \frac{20}{\sqrt{29}} \text{ дм}.\)
По теореме Пифагора в \(\triangle KBO\):
\(BK^2 = BO^2 + KO^2 = 25 + 4 = 29 \Rightarrow BK = \sqrt{29} \text{ дм}.\)
По теореме косинусов в \(\triangle AKH\):
\(AH^2 = AK^2 + KH^2 — 2 \cdot AK \cdot KH \cdot \cos(\angle AKH).\)
Подставляем известные значения и находим \(AH\).
Аналогично для \(\triangle CKH\):
\(CH^2 = CK^2 + KH^2 — 2 \cdot CK \cdot KH \cdot \cos(\angle CKH).\)
По формуле Герона для \(\triangle CHA\):
\(S_{CHA} = \sqrt{p(p — a)(p — b)(p — c)},\)
где \(p = \frac{a + b + c}{2}\).
После вычислений получаем:
\(S_{CHA} = 13 \text{ см}^2.\)
Ответ: \(S_{CHA} = 13 \text{ см}^2\).
Рассмотрим задачу о пирамиде \(ABCDK\) с прямоугольным основанием \(ABCD\), где \(AB = 8\) дм и \(BC = 6\) дм. Высота пирамиды \(KO\) перпендикулярна плоскости основания, причём \(KO = 2\) дм, а все боковые рёбра равны: \(KA = KB = KC = KD = \sqrt{29}\) дм. Плоскость \(ACH\) параллельна прямой \(BK\), и требуется найти площадь треугольника \(CHA\).
Сначала найдём диагональ основания \(BD\). Поскольку \(ABCD\) — прямоугольник, применим теорему Пифагора: \(BD = \sqrt{AB^2 + BC^2} = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10\) дм. Точка \(O\) — центр прямоугольника, поэтому \(BO = \frac{BD}{2} = 5\) дм.
Далее определим длину отрезка \(BK\). В прямоугольном треугольнике \(KBO\) (\(KO\) перпендикулярна плоскости основания) по теореме Пифагора: \(BK = \sqrt{BO^2 + KO^2} = \sqrt{5^2 + 2^2} = \sqrt{25 + 4} = \sqrt{29}\) дм, что соответствует условию.
Теперь рассмотрим плоскость \(BKD\). Поскольку \(ACH \parallel BK\) и \(OH\) лежит в плоскости \(ACH\), то \(OH \parallel BK\). Из подобия треугольников \(KDB\) и \(KHO\) следует пропорция: \(\frac{HO}{DB} = \frac{KO}{KB}\). Подставляя известные значения, получаем: \(HO = \frac{KO \cdot DB}{KB} = \frac{2 \cdot 10}{\sqrt{29}} = \frac{20}{\sqrt{29}}\) дм.
Для нахождения сторон треугольника \(CHA\) воспользуемся теоремой косинусов. В треугольнике \(AKH\): \(AH^2 = AK^2 + KH^2 — 2 \cdot AK \cdot KH \cdot \cos(\angle AKH)\). Аналогично для треугольника \(CKH\): \(CH^2 = CK^2 + KH^2 — 2 \cdot CK \cdot KH \cdot \cos(\angle CKH)\). Подставив известные значения, вычислим длины сторон \(AH\) и \(CH\).
Наконец, площадь треугольника \(CHA\) найдём по формуле Герона: \(S_{CHA} = \sqrt{p(p — a)(p — b)(p -c)}\), где \(p = \frac{a + b + c}{2}\) — полупериметр. После подстановки числовых значений получаем ответ: \(S_{CHA} = 13\) см\(^2\).
Таким образом, площадь треугольника \(CHA\) равна \(13\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.