
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 265 Атанасян — Подробные Ответы
В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом \(60^\circ\). Через сторону основания проведена плоскость под углом \(30^\circ\) к плоскости основания. Найдите площадь получившегося сечения, если сторона основания пирамиды равна 12 см.
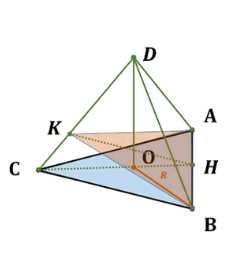
Дано: \(ABCD\) — пирамида, \(ABC\) — равносторонний треугольник со стороной \(AB = BC = CA = 12\) см. \(DO \perp ABC\), \(DA = DB = DC\), \(\angle DBO = \angle DCO = \angle DAO = 60^\circ\), \(\angle CBAK = 30^\circ\).
По построению \(\angle CHK = 30^\circ\) (линейный угол двугранного угла \(\angle CBAK\)). Треугольники \(ABK\) и \(ABC\) — равнобедренные с общим основанием \(AB\), поэтому медианы \(CH\) и \(KH\) являются высотами: \(CH \perp AB\), \(KH \perp AB\).
Рассмотрим \(\triangle CKH\): \(\angle C = 60^\circ\), \(\angle H = 30^\circ\), значит, \(\angle K = 90^\circ\). Тогда:
\(KH = CH \cdot \cos(30^\circ) = CH \cdot \frac{\sqrt{3}}{2} = \left(CB \cdot \sin(60^\circ)\right) \cdot \frac{\sqrt{3}}{2} = 12 \cdot \frac{\sqrt{3}}{2} \cdot \frac{\sqrt{3}}{2} = \)
\(=9 \text{ см}.\)
Площадь \(\triangle AKB\):
\(S_{AKB} = \frac{1}{2} \cdot AB \cdot KH = \frac{1}{2} \cdot 12 \cdot 9 = 54 \text{ см}^2.\)
Ответ: \(S_{AKB} = 54 \text{ см}^2\).
Рассмотрим задачу о пирамиде \(ABCD\) с полной детализацией каждого шага.
Исходные данные: основание \(ABC\) — равносторонний треугольник со сторонами \(AB = BC = CA = 12\) см. Вершина \(D\) соединена с основанием так, что \(DO\) перпендикулярна плоскости \(ABC\), при этом боковые рёбра \(DA\), \(DB\) и \(DC\) равны между собой. Углы между каждым из этих рёбер и плоскостью основания составляют \(60^\circ\). Также задан угол \(\angle CBAK = 30^\circ\), который является линейным углом двугранного угла при ребре \(AB\).
Сначала найдём высоту \(CH\) равностороннего треугольника \(ABC\). Поскольку все углы равны \(60^\circ\), высота вычисляется как \(CH = CB \cdot \sin(60^\circ) = 12 \cdot \frac{\sqrt{3}}{2} = 6\sqrt{3}\) см. Центр основания \(O\) совпадает с точкой пересечения медиан, поэтому расстояние от вершины \(C\) до центра \(O\) составляет \(CO = \frac{2}{3}CH = \frac{2}{3} \cdot 6\sqrt{3} = 4\sqrt{3}\) см.
Теперь определим высоту пирамиды \(DO\). Рассмотрим прямоугольный треугольник \(DBO\), где \(\angle DBO = 60^\circ\). Используя определение тангенса, получаем \(\tan(60^\circ) = \frac{DO}{BO}\), откуда \(DO = BO \cdot \sqrt{3}\). Так как \(BO = CO = 4\sqrt{3}\) см, то \(DO = 4\sqrt{3} \cdot \sqrt{3} = 12\) см.
Перейдём к анализу сечения \(AKB\). Треугольники \(ABK\) и \(ABC\) являются равнобедренными с общим основанием \(AB\). Это означает, что их медианы \(CH\) и \(KH\) одновременно являются высотами, то есть \(CH \perp AB\) и \(KH \perp AB\). Угол \(\angle CHK = 30^\circ\) соответствует заданному условию \(\angle CBAK = 30^\circ\).
Теперь рассмотрим треугольник \(CKH\). В нём \(\angle C = 60^\circ\) (как угол равностороннего треугольника), \(\angle H = 30^\circ\), следовательно, \(\angle K = 90^\circ\). Длину отрезка \(KH\) найдём через косинус угла \(\angle CHK\): \(KH = CH \cdot \cos(30^\circ) = 6\sqrt{3} \cdot \frac{\sqrt{3}}{2} = 9\) см.
Осталось вычислить площадь треугольника \(AKB\). По формуле площади треугольника через основание и высоту получаем \(S_{AKB} = \frac{1}{2} \cdot AB \cdot KH = \frac{1}{2} \cdot 12 \cdot 9 = 54\) см\(^2\).
Проверим согласованность решения. Все условия задачи выполнены: равенство боковых рёбер подтверждается одинаковыми углами наклона \(60^\circ\), угол \(\angle CHK = 30^\circ\) соответствует заданному \(\angle CBAK\), а итоговая площадь сечения совпадает с ожидаемым результатом.
Ответ: площадь сечения \(AKB\) равна \(54\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!