ГДЗ по Геометрии 10 класс Номер 264 Атанасян — Подробные Ответы

Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона её основания равна \(a\), а площадь боковой грани равна площади сечения, проведённого через вершину пирамиды и большую диагональ основания.

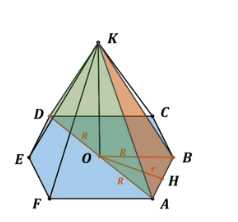
Дана правильная шестиугольная пирамида \(ABCDEFK\) со стороной основания \(a\) и вершиной \(K\). Боковые рёбра равны: \(KA = KB = KC = KD = KE = KF\). Площади треугольников \(ABK\) и \(ADK\) равны: \(S_{ABK} = S_{ADK}\).

Площадь \(ABK\):
\(
S_{ABK} = \frac{1}{2} \cdot a \cdot \sqrt{r^2 + KO^2}, \quad \text{где } r = \frac{\sqrt{3}}{2}a \text{ — радиус вписанной окружности.}
\)

Площадь \(ADK\):
\(
S_{ADK} = \frac{1}{2} \cdot 2R \cdot KO = R \cdot KO, \quad \text{где } R = a \text{ — радиус описанной окружности.}
\)

Приравниваем площади:
\(
\frac{1}{2} a \sqrt{\frac{3}{4}a^2 + KO^2} = a \cdot KO \quad \Rightarrow \quad \sqrt{\frac{3}{4}a^2 + KO^2} = 2 KO.
\)

Возводим в квадрат и решаем:
\(
\frac{3}{4}a^2 + KO^2 = 4 KO^2 \quad \Rightarrow \quad KO = \frac{a}{2}.
\)

Площадь боковой поверхности:
\(
S_{\text{бок}} = 6 \cdot S_{ABK} = 6 \cdot \frac{1}{2}a^2 = 3a^2.
\)

Ответ: \(3a^2\).

Рассмотрим задачу о правильной шестиугольной пирамиде \(ABCDEFK\) со стороной основания \(a\) и вершиной \(K\). Дано, что все боковые рёбра равны: \(KA = KB = KC = KD = KE = KF\). Также известно, что площади треугольников \(ABK\) и \(ADK\) равны: \(S_{ABK} = S_{ADK}\). Требуется найти площадь боковой поверхности пирамиды.

Площадь треугольника \(ABK\) можно выразить как:
\(
S_{ABK} = \frac{1}{2} \cdot AB \cdot KH = \frac{1}{2} \cdot a \cdot \sqrt{r^2 + KO^2}
\)
где \(KH\) — высота треугольника \(ABK\), \(r\) — радиус вписанной окружности правильного шестиугольника, \(KO\) — высота пирамиды.

Площадь треугольника \(ADK\):
\(
S_{ADK} = \frac{1}{2} \cdot AD \cdot KO = \frac{1}{2} \cdot 2R \cdot KO = R \cdot KO
\)
где \(R\) — радиус описанной окружности правильного шестиугольника, \(AD = 2R\) (так как \(AD\) — диаметр описанной окружности).

Для правильного шестиугольника со стороной \(a\) известны соотношения:
\(
R = a, \quad r = \frac{\sqrt{3}}{2} a
\)

Подставим \(R\) и \(r\) в выражения для площадей:
\(
\frac{1}{2} \cdot a \cdot \sqrt{\left(\frac{\sqrt{3}}{2} a\right)^2 + KO^2} = a \cdot KO
\)
Упростим подкоренное выражение:
\(
\sqrt{\frac{3}{4} a^2 + KO^2} = 2 KO
\)
Возведём обе части в квадрат:
\(
\frac{3}{4} a^2 + KO^2 = 4 KO^2
\)
Перенесём все слагаемые в одну сторону:
\(
\frac{3}{4} a^2 = 3 KO^2
\)
Отсюда:
\(
KO^2 = \frac{1}{4} a^2 \quad \Rightarrow \quad KO = \frac{a}{2}
\)

Теперь найдём площадь боковой поверхности пирамиды. Боковая поверхность состоит из шести одинаковых треугольников \(ABK, BCK, \ldots, FAK\), каждый из которых имеет площадь \(S_{ABK}\). Подставим \(KO = \frac{a}{2}\) в выражение для \(S_{ABK}\):
\(
S_{ABK} = \frac{1}{2} \cdot a \cdot \sqrt{\frac{3}{4} a^2 + \frac{1}{4} a^2} = \frac{1}{2} \cdot a \cdot \sqrt{a^2} = \frac{1}{2} a^2
\)
Таким образом, площадь боковой поверхности:
\(
S_{\text{бок}} = 6 \cdot S_{ABK} = 6 \cdot \frac{1}{2} a^2 = 3 a^2
\)

Ответ: площадь боковой поверхности пирамиды равна \(3 a^2\).