
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 263 Атанасян — Подробные Ответы
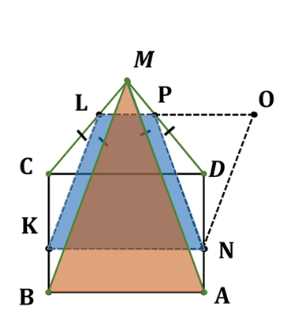
В правильной пирамиде \(MABCD\) точки \(K\), \(L\) и \(N\) лежат соответственно на рёбрах \(BC\), \(MC\) и \(AD\), причём \(KN \parallel BA\), \(KL \parallel BM\).
а) Постройте сечение пирамиды плоскостью \(KLN\) и определите вид сечения.
б) Докажите, что плоскость \(KLN\) параллельна плоскости \(AMB\).
Решение:
Дано: \(ABCDM\) — правильная пирамида, \(M\) — вершина, \(MA = MB = MC = MD\), \(K \in BC\), \(L \in CM\), \(N \in AD\), \(KL \parallel MB\), \(KN \parallel AB\).
Построение:
1. \(LO \parallel KN\), \(LK \parallel ON\) \(\Rightarrow\) \(KLON\) — параллелограмм.
2. \(P = LO \cap MD\), \(PN\) — линия сечения.
Доказательство параллельности плоскостей:
Плоскости \(KLN\) и \(ABM\) параллельны по признаку: если две пересекающиеся прямые одной плоскости (\(KL\) и \(KN\)) соответственно параллельны двум прямым другой плоскости (\(MB\) и \(AB\)), то плоскости параллельны.
Результат: сечение \(KLPN\) — трапеция.
Ответ: сечение \(KLPN\) — трапеция.
Рассмотрим решение задачи о построении сечения в правильной пирамиде \(ABCDM\) с вершиной \(M\), где \(MA = MB = MC = MD\). Точки \(K\), \(L\), \(N\) расположены на рёбрах или сторонах: \(K\) лежит на \(BC\), \(L\) на \(CM\), \(N\) на \(AD\). Условия параллельности заданы как \(KL \parallel MB\) и \(KN \parallel AB\).
Сначала анализируем геометрическую конфигурацию. Поскольку \(KN \parallel AB\), а \(AB\) принадлежит основанию \(ABCD\), то \(KN\) либо лежит в плоскости основания, либо параллельна ей. Учитывая, что \(KL \parallel MB\), а \(MB\) является боковым ребром пирамиды, направление \(KL\) совпадает с направлением этого ребра.
Для построения сечения вводим вспомогательную прямую \(LO\), параллельную \(KN\). Так как \(KN \parallel AB\), то \(LO\) также параллельна \(AB\). Теперь рассматриваем четырёхугольник \(KLON\). По построению \(KL \parallel MB\) и \(ON\) (часть \(LO\)) параллельна \(AB\), следовательно, \(KLON\) является параллелограммом, так как его противоположные стороны попарно параллельны.
Далее находим точку пересечения \(P = LO \cap MD\). Поскольку \(LO\) лежит в плоскости сечения, а \(MD\) является ребром пирамиды, точка \(P\) принадлежит и сечению, и ребру \(MD\). Проведя отрезок \(PN\), получаем искомое сечение \(KLPN\).
Доказательство параллельности плоскостей \(KLN\) и \(ABM\) основано на признаке параллельности: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны. В данном случае \(KL \parallel MB\) и \(KN \parallel AB\), причём \(MB\) и \(AB\) лежат в плоскости \(ABM\) и пересекаются в точке \(B\), а \(KL\) и \(KN\) лежат в плоскости \(KLN\) и пересекаются в точке \(K\). Таким образом, плоскости \(KLN\) и \(ABM\) параллельны.
Форма сечения \(KLPN\) определяется как трапеция, поскольку \(KL \parallel PN\) (по построению \(LO \parallel KN\), а \(PN\) является продолжением \(LO\)), а стороны \(KN\) и \(LP\) не параллельны.
Итоговый вывод: построенное сечение \(KLPN\) представляет собой трапецию, параллельную плоскости \(ABM\), что подтверждается геометрическими построениями и признаком параллельности плоскостей.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!