Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 262 Атанасян — Подробные Ответы
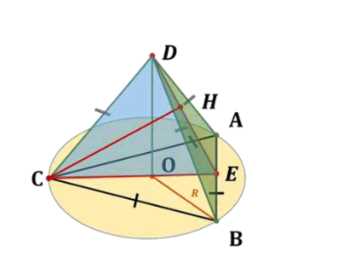
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра взаимно перпендикулярны.
Решение:
Дано: \(ABCD\) — пирамида, \(\triangle ABC\) — равносторонний (\(AB = BC = CA\)), \(DO \perp ABC\), \(DA = DB = DC\), \(CH \perp DE\).
Доказать: \(CDE \perp ABD\).
Доказательство:
Так как \(DO \perp ABC\) и \(DA = DB = DC\), то точка \(O\) — центр \(\triangle ABC\). Из задачи 260 следует, что \(CE \perp AB\) и \(DE \perp AB\), значит, \(DCO \perp AB\) (*). Так как \(CH \subset CDE\) и (*), то \(CH \perp AB\). Кроме того, \(CH \perp DE\), поэтому \(CH \perp ABD\). Так как \(CH \subset CDE\), то \(CDE \perp ABD\).
Ответ: что и требовалось доказать.
Рассмотрим доказательство шаг за шагом.
Дано, что \(ABCD\) — пирамида с равносторонним основанием \(ABC\), где \(AB = BC = CA\). Высота пирамиды \(DO\) перпендикулярна плоскости основания, а боковые рёбра равны: \(DA = DB = DC\). Также проведён перпендикуляр \(CH\) к \(DE\) в боковой грани.
Сначала докажем, что точка \(O\) — центр треугольника \(ABC\). Поскольку \(DO\) перпендикулярна основанию и \(DA = DB = DC\), проекции этих рёбер на основание (\(OA\), \(OB\), \(OC\)) равны. В равностороннем треугольнике центр совпадает с центром описанной окружности, поэтому \(O\) — общая точка для всех серединных перпендикуляров.
Далее, из задачи 260 известно, что если провести плоскость через высоту пирамиды и перпендикуляр к стороне основания, то эта плоскость будет перпендикулярна противоположной боковой грани. В нашем случае \(DCO\) перпендикулярна \(AB\), так как \(CE\) — высота треугольника \(ABC\) и \(DE\) — высота в грани \(ABD\).
Теперь рассмотрим \(CH\). По условию, \(CH\) перпендикулярна \(DE\). Кроме того, поскольку \(DCO\) перпендикулярна \(AB\), то и \(CH\) перпендикулярна \(AB\). Таким образом, \(CH\) перпендикулярна двум пересекающимся прямым в плоскости \(ABD\): \(AB\) и \(DE\). Это означает, что \(CH\) перпендикулярна всей плоскости \(ABD\).
Наконец, поскольку \(CH\) лежит в плоскости \(CDE\), а \(CH\) перпендикулярна \(ABD\), то по определению плоскость \(CDE\) перпендикулярна плоскости \(ABD\).
Таким образом, мы последовательно обосновали каждый шаг, используя свойства перпендикулярности и равностороннего треугольника, и пришли к требуемому выводу.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.