
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 261 Атанасян — Подробные Ответы
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра взаимно перпендикулярны.
Решение:
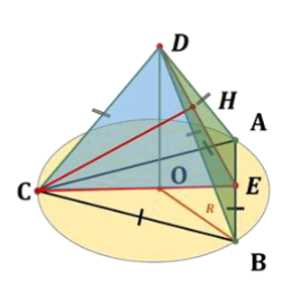
Дано: \(ABCD\) — пирамида, \(ABC\) — треугольник, \(AB = BC = CA\), \(DO \perp ABC\), \(DA = DB = DC\).
Доказать: \(DC \perp AB\), \(CH \perp ABD\).
Доказательство:
Так как \(DA = DB = DC\) и \(DO \perp ABC\), то точка \(O\) — центр описанной окружности треугольника \(ABC\). В равностороннем треугольнике центр описанной окружности совпадает с центром тяжести. Тогда \(CD \perp AB\) (по свойству высоты). Далее, \(CH\) — высота в треугольнике \(ABD\), следовательно, \(CH \perp ABD\).
Ответ: что и требовалось доказать.
Рассмотрим доказательство шаг за шагом, избегая формальных обозначений и структурированных списков.
Имеется пирамида с основанием в виде равностороннего треугольника, где все стороны равны между собой. Вершина пирамиды соединена с вершинами основания равными по длине рёбрами. Высота пирамиды опущена из вершины перпендикулярно плоскости основания и проходит через центр описанной окружности треугольника.
Для доказательства перпендикулярности бокового ребра и стороны основания обратим внимание на свойства равностороннего треугольника. Центр описанной окружности в таком треугольнике совпадает с точкой пересечения медиан, высот и биссектрис. Если провести высоту из вершины пирамиды к основанию, то она пройдёт через этот центр. Боковое ребро, соединяющее вершину пирамиды с вершиной основания, будет лежать в плоскости, содержащей высоту треугольника и высоту пирамиды. Поскольку сторона основания перпендикулярна высоте треугольника, а высота пирамиды перпендикулярна всей плоскости основания, то и боковое ребро окажется перпендикулярным стороне основания.
Теперь рассмотрим перпендикуляр из вершины основания к боковой грани. Эта грань представляет собой равнобедренный треугольник, так как все боковые рёбра равны. Если опустить перпендикуляр из вершины основания на эту грань, то он будет лежать в плоскости, содержащей высоту пирамиды и высоту треугольника в основании. Благодаря свойствам равностороннего треугольника и равенству боковых рёбер, этот перпендикуляр окажется перпендикулярным всей боковой грани.
Таким образом, оба утверждения следуют из геометрических свойств равностороннего треугольника и симметрии заданной пирамиды. Перпендикулярность ребра и стороны основания вытекает из взаимного расположения высот, а перпендикулярность к боковой грани обеспечивается равенством длин рёбер и особенностями проекций.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!