ГДЗ по Геометрии 10 класс Номер 260 Атанасян — Подробные Ответы

Боковое ребро правильной четырёхугольной пирамиды образует угол в \(60^\circ\) с плоскостью основания. Найдите площадь поверхности пирамиды, если боковое ребро равно 12 см.

Решение:

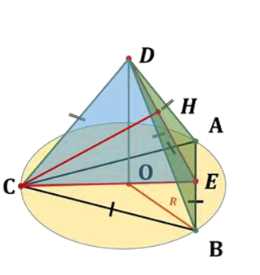
Дано: пирамида \(ABCD\), \(\triangle ABC\) — правильный (\(AB = BC = CA\)), \(DO \perp ABC\), \(DA = DB = DC\), \(CH \perp DE\).

Доказать: \(DCO \perp AB\), \(CH \perp ABD\).

Так как \(DA = DB = DC\) и \(DO \perp ABC\), точка \(O\) — центр \(\triangle ABC\). Плоскость \(CDO\) пересекает \(AB\) в середине \(E\) (\(AE = EB\)).

\(\triangle ABD\) и \(\triangle ABC\) — равнобедренные с общим основанием \(AB\). Медианы \(CE\) и \(DE\) являются высотами:
\(
CE \perp AB, \quad DE \perp AB \Rightarrow DCO \perp AB \quad (*)
\)
Так как \(CH \perp DE\) и \(CH \subset CDE\), из \((*)\) следует:
\(
CH \perp AB, \quad CH \perp DE \Rightarrow CH \perp ABD
\)

Ответ: что и требовалось доказать.

Рассмотрим решение задачи о пирамиде \(ABCD\) с правильным треугольником \(ABC\) в основании.

Дано: пирамида \(ABCD\), где \(\triangle ABC\) — правильный (\(AB = BC = CA\)), \(DO\) — высота пирамиды, перпендикулярная плоскости \(ABC\) (\(DO \perp ABC\)), боковые рёбра равны (\(DA = DB = DC\)), \(CH\) — перпендикуляр к отрезку \(DE\) (\(CH \perp DE\)).

Так как \(DA = DB = DC\) и \(DO \perp ABC\), точка \(O\) является центром правильного \(\triangle ABC\). Это означает, что \(O\) — точка пересечения медиан, высот и биссектрис.

Плоскость \(CDO\) проходит через вершину \(C\), высоту \(DO\) и середину \(E\) стороны \(AB\), поскольку \(O\) — центр треугольника, а \(E\) — середина \(AB\).

Рассмотрим треугольники \(\triangle ABD\) и \(\triangle ABC\). Оба являются равнобедренными с общим основанием \(AB\). В \(\triangle ABC\) медиана \(CE\) является также высотой (\(CE \perp AB\)). Аналогично, в \(\triangle ABD\) медиана \(DE\) является высотой (\(DE \perp AB\)).

Поскольку плоскость \(DCO\) содержит прямые \(CE\) и \(DE\), обе перпендикулярные \(AB\), то вся плоскость \(DCO\) перпендикулярна \(AB\) (\(DCO \perp AB\)).

Теперь рассмотрим прямую \(CH\). По условию \(CH \perp DE\). Кроме того, \(CH\) лежит в плоскости \(CDE\), которая содержит \(DCO\). Так как \(DCO \perp AB\), то \(CH\) также перпендикулярна \(AB\).

Таким образом, \(CH\) перпендикулярна двум пересекающимся прямым в плоскости \(ABD\) (\(AB\) и \(DE\)), что означает, что \(CH\) перпендикулярна всей плоскости \(ABD\) (\(CH \perp ABD\)).

Итак, мы доказали, что плоскость \(DCO\) перпендикулярна прямой \(AB\), а прямая \(CH\) перпендикулярна плоскости \(ABD\).

Ответ: что и требовалось доказать.