
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 26 Атанасян — Подробные Ответы
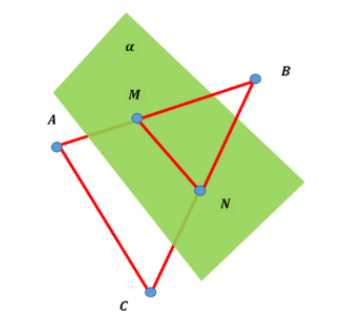
Сторона \(AC\) треугольника \(ABC\) параллельна плоскости \(\alpha\), а стороны \(AB\) и \(BC\) пересекаются с этой плоскостью в точках \(M\) и \(N\). Докажите, что треугольники \(ABC\) и \(MNB\) подобны.
Дано: \( AC \parallel \alpha \), \( M \in AB \), \( N \in BC \), \( MN \parallel AC \).
Поскольку \( MN \parallel AC \), плоскость \( \alpha \) пересекает треугольник \( \triangle ABC \) линией, параллельной стороне \( AC \).
Из свойства пересечения треугольника плоскостью, параллельной одной из его сторон, следует, что \( \triangle ABC \sim \triangle MNB \).
Угол \( \angle ABC \) общий для \( \triangle ABC \) и \( \triangle MNB \), а углы \( \angle BAC \) и \( \angle MNB \) равны как внутренние односторонние углы.
Следовательно, \( \triangle ABC \sim \triangle MNB \).
Дано:
Треугольник \( \triangle ABC \), сторона \( AC \parallel \alpha \), точки \( M \) и \( N \) — точки пересечения прямых \( AB \) и \( BC \) соответственно с плоскостью \( \alpha \).
Требуется доказать, что \( \triangle ABC \sim \triangle MNB \).
Решение:
1. Рассмотрим условия задачи. Известно, что \( AC \parallel \alpha \). Это означает, что сторона \( AC \) не пересекает плоскость \( \alpha \). Также прямые \( AB \) и \( BC \) пересекают плоскость \( \alpha \) в точках \( M \) и \( N \), соответственно.
2. Поскольку \( M \in AB \) и \( N \in BC \), отрезок \( MN \) лежит в плоскости \( \alpha \). По условию задачи, \( MN \parallel AC \).
3. Используем свойство пересечения треугольника плоскостью, параллельной одной из его сторон. Если плоскость пересекает треугольник так, что линия пересечения плоскости с треугольником параллельна одной из сторон треугольника, то треугольники, образованные этим пересечением, подобны.
4. В данном случае \( MN \parallel AC \), следовательно, треугольники \( \triangle ABC \) и \( \triangle MNB \) подобны. Это следует из признака подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то такие треугольники подобны.
5. Докажем равенство углов:
Угол \( \angle ABC \) общий для треугольников \( \triangle ABC \) и \( \triangle MNB \).
Углы \( \angle BAC \) и \( \angle MNB \) равны как углы, образованные параллельными прямыми \( AC \) и \( MN \) и секущими \( AB \) и \( BC \) (по свойству внутренних односторонних углов).
6. Таким образом, треугольники \( \triangle ABC \) и \( \triangle MNB \) подобны по признаку: два угла одного треугольника равны двум углам другого треугольника.
Ответ:
\( \triangle ABC \sim \triangle MNB \), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!