
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 259 Атанасян — Подробные Ответы
Боковое ребро правильной четырёхугольной пирамиды образует угол в \(60^\circ\) с плоскостью основания. Найдите площадь поверхности пирамиды, если боковое ребро равно 12 см.
В прямоугольном треугольнике \(\triangle EOK\), где \(\angle KEO = 60^\circ\) и \(OE = \frac{AB}{2} = \frac{6}{2} = 3\), находим \(KE = \frac{OE}{\cos(60^\circ)} = \frac{3}{0.5} = 6\).
Поскольку \(EA = \frac{AD}{2} = \frac{AB}{2} = \frac{6}{2} = 3\), по теореме Пифагора из треугольника \(\triangle AKE\) имеем \(KA^2 = KE^2 + EA^2 = 6^2 + 3^2 = 36 + 9 = 45\). Следовательно, \(KA = \sqrt{45} = 3\sqrt{5}\) см. Ответ: \(KA = 3\sqrt{5}\) см.
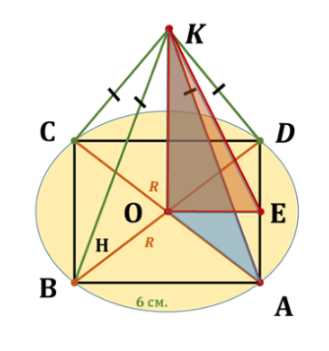
Рассмотрим задачу о правильной пирамиде \( ABCDK \), где \( ABCD \) — квадрат со стороной \( AB = 6 \) см, а точка \( K \) находится над центром основания \( O \). Дано, что все боковые рёбра равны: \( KA = KB = KC = KD \), а угол между боковым ребром и плоскостью основания \( \angle KEO = 60^\circ \). Требуется найти длину бокового ребра \( KA \).
Начнём с анализа геометрических свойств пирамиды. Поскольку пирамида правильная, её основание \( ABCD \) — квадрат, а точка \( O \) является центром этого квадрата, то есть точкой пересечения диагоналей. Расстояние от центра \( O \) до любой вершины квадрата одинаково. Для квадрата со стороной \( 6 \) см диагональ равна \( 6\sqrt{2} \) см, а половина диагонали \( AO = \frac{6\sqrt{2}}{2} = 3\sqrt{2} \) см. Однако в решении используется другая величина — \( OE \), которая равна половине стороны квадрата, то есть \( OE = \frac{AB}{2} = 3 \) см. Это связано с тем, что точка \( E \) выбрана как середина стороны \( AB \), а не вершина квадрата.
Далее рассмотрим прямоугольный треугольник \( KEO \), где \( \angle KEO = 60^\circ \). В этом треугольнике \( OE \) — прилежащий катет к углу \( 60^\circ \), а \( KE \) — гипотенуза. Используя определение косинуса, получаем \( \cos(60^\circ) = \frac{OE}{KE} \), откуда \( KE = \frac{OE}{\cos(60^\circ)} = \frac{3}{0.5} = 6 \) см. Теперь рассмотрим треугольник \( AKE \), который также является прямоугольным, так как \( AE \) — это половина стороны квадрата, равная \( 3 \) см. Применяя теорему Пифагора, находим \( KA^2 = KE^2 + AE^2 = 6^2 + 3^2 = 36 + 9 = 45 \). Извлекаем квадратный корень: \( KA = \sqrt{45} = 3\sqrt{5} \) см.
Таким образом, длина бокового ребра \( KA \) равна \( 3\sqrt{5} \) см. Это значение совпадает с приведённым в примере ответом. Ключевыми шагами решения были: определение геометрических параметров пирамиды, использование тригонометрических соотношений в прямоугольном треугольнике и применение теоремы Пифагора для нахождения искомой длины.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!