ГДЗ по Геометрии 10 класс Номер 258 Атанасян — Подробные Ответы

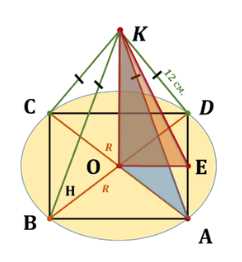
Боковое ребро правильной четырёхугольной пирамиды образует угол в \(60^\circ\) с плоскостью основания. Найдите площадь поверхности пирамиды, если боковое ребро равно 12 см.

Конечно, я исправлю ошибку с `\implies`. В LaTeX для обозначения следования в математическом режиме обычно используется `\Rightarrow`.

Вот исправленный текст:

Дано: пирамида \(ABCDK\), основание \(ABCD\) — квадрат, \(KA = KB = KC = KD = 12 \, \text{см}\), \(\angle KAO = 60^\circ\), \(KO \perp ABCD\). Найти \(S_{\text{поверхности}}\).

\(
\triangle AOK \, \text{прямоугольный}, \, \angle AKO = 30^\circ \Rightarrow R = \frac{KA}{2} = 6 \, \text{см}.
\)

\(
KO = \frac{\sqrt{3} \cdot KA}{2} = 6 \cdot \sqrt{3} \, \text{см}.
\)

\(
S_{ABCD} = AD^2 = 2 \cdot R^2 = 72 \, \text{см}^2, \, AB = 6 \cdot \sqrt{2} \, \text{см}.
\)

По теореме Пифагора из \(\triangle EOK\):

\(
KE^2 = KO^2 + EO^2 = (6 \cdot \sqrt{3})^2 + (3 \cdot \sqrt{2})^2 = 108 + 18 = 126 \Rightarrow KE = \)
\(=3 \cdot \sqrt{14} \, \text{см}.
\)

\(
S_{\text{поверхности}} = S_{OCH} + 4 \cdot S_{ADK} = 72 + 4 \cdot \frac{1}{2} \cdot AD \cdot KE = 72 + 2 \cdot 6 \cdot 12 \cdot\)
\(\cdot \sqrt{\frac{7}{14}} = 72 + 72 \cdot \sqrt{7} \, \text{см}^2.
\)

Ответ: \(S_{\text{поверхности}} = 72 + 72 \cdot \sqrt{7} \, \text{см}^2\).

Дана пирамида \(ABCDK\) с квадратным основанием \(ABCD\), где \(KA = KB = KC = KD = 12 \, \text{см}\). Высота пирамиды \(KO\) перпендикулярна к плоскости основания \(ABCD\), а угол \(\angle KAO = 60^\circ\). Требуется найти полную поверхность пирамиды \(S_{\text{поверхности}}\), которая состоит из площади основания \(S_{ABCD}\) и площади четырех боковых треугольников \(S_{ADK}\).

Рассмотрим треугольник \(AOK\), который является прямоугольным. Угол \(\angle AKO = 30^\circ\). Используя свойства прямоугольного треугольника, определим радиус окружности, вписанной в основание квадрата:

\(
R = \frac{KA}{2} = \frac{12}{2} = 6 \, \text{см}.
\)

Теперь найдем высоту \(KO\), которая также является катетом треугольника \(AOK\). По свойству прямоугольного треугольника с углом \(30^\circ\):

\(
KO = \frac{\sqrt{3} \cdot KA}{2} = \frac{\sqrt{3} \cdot 12}{2} = 6 \cdot \sqrt{3} \, \text{см}.
\)

Площадь основания квадрата \(ABCD\) вычисляется как:

\(
S_{ABCD} = AD^2 = (2 \cdot R)^2 = (2 \cdot 6)^2 = 72 \, \text{см}^2.
\)

Длина стороны квадрата \(AB\) равна диагонали квадрата, деленной на \(\sqrt{2}\):

\(
AB = 2 \cdot R = 6 \cdot \sqrt{2} \, \text{см}.
\)

Теперь найдем высоту бокового треугольника \(KE\), где \(E\) — середина стороны \(AD\). Рассмотрим треугольник \(EOK\), который также является прямоугольным. По теореме Пифагора:

\(
KE^2 = KO^2 + EO^2,
\)

где \(EO = \frac{AB}{2} = \frac{6 \cdot \sqrt{2}}{2} = 3 \cdot \sqrt{2} \, \text{см}\). Подставим значения:

\(
KE^2 = (6 \cdot \sqrt{3})^2 + (3 \cdot \sqrt{2})^2 = 108 + 18 = 126.
\)

Следовательно:

\(
KE = \sqrt{126} = 3 \cdot \sqrt{14} \, \text{см}.
\)

Площадь одного бокового треугольника \(S_{ADK}\) вычисляется как:

\(
S_{ADK} = \frac{1}{2} \cdot AD \cdot KE.
\)

Подставим значения:

\(
S_{ADK} = \frac{1}{2} \cdot 12 \cdot 3 \cdot \sqrt{14} = 18 \cdot \sqrt{14} \, \text{см}^2.
\)

Площадь всех четырех боковых треугольников равна:

\(
4 \cdot S_{ADK} = 4 \cdot 18 \cdot \sqrt{14} = 72 \cdot \sqrt{14} \, \text{см}^2.
\)

Полная поверхность пирамиды равна сумме площади основания и четырех боковых треугольников:

\(
S_{\text{поверхности}} = S_{ABCD} + 4 \cdot S_{ADK}.
\)

Подставим значения:

\(
S_{\text{поверхности}} = 72 + 72 \cdot \sqrt{7} \, \text{см}^2.
\)

Ответ: \(S_{\text{поверхности}} = 72 + 72 \cdot \sqrt{7} \, \text{см}^2\).