
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 256 Атанасян — Подробные Ответы
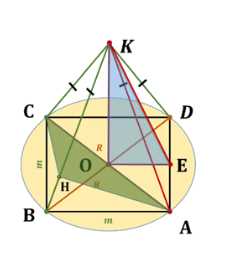
В правильной четырёхугольной пирамиде сторона основания равна \(m\), а плоский угол при вершине равен \(\omega\). Найдите:
а) высоту пирамиды;
б) боковое ребро пирамиды;
в) угол между боковой гранью и плоскостью основания;
г) двугранный угол при боковом ребре пирамиды
Дано: пирамида \(ABCDK\), основание \(ABCD\) — квадрат со стороной \(m\), высота \(KO\) перпендикулярна \(ABCD\), \(KA = KB = KC = KD\), угол \(\angle AKB = \alpha\).
Найти:
а) \(KO\),
б) \(KA\),
в) \(\angle OEK\),
г) \(\cos(\angle CBAK)\).
Решение:
Диагональ квадрата:
\(
R = \frac{m \cdot \sqrt{2}}{2}.
\)
Пусть \(OK = x\), \(AK = y\).
По теореме Пифагора для \(\triangle AOK\):
\(
\frac{m^2}{2} + x^2 = y^2. \tag{1}
\)
По теореме косинусов для \(\triangle AKB\):
\(
m^2 = y^2 + y^2 — 2 \cdot y \cdot y \cdot \cos(\alpha),
\)
откуда
\(
\cos(\alpha) = 1 — \frac{m^2}{2 \cdot y^2}. \tag{2}
\)
Подставим (2) в (1):
\(
x^2 = \frac{m^2}{2 — 2 \cdot \cos(\alpha)} = \frac{m^2}{2 \cdot (1 — \cos(\alpha))}.
\)
Отсюда:
\(
x = \frac{m}{\sqrt{2 \cdot (1 — \cos(\alpha))}}.
\)
\(
y = \frac{m}{\sqrt{1 — \cos(\alpha)}}.
\)
Угол \(\angle OEK\):
\(
\tan(\angle OEK) = \frac{2 \cdot x}{m}, \quad \cos(\angle OEK) = \frac{2 \cdot \cos(\alpha)}{\sqrt{1 — \cos(\alpha)}}.
\)
По теореме Пифагора для \(\triangle ANB\):
\(
AH^2 = m^2 — z^2 = m^2 — \frac{m^2 \cdot (1 + \cos(\alpha))}{4}.
\)
По теореме косинусов для \(\triangle CHA\):
\(
\cos(\angle CBAK) = 1 — \frac{m^2 \cdot (1 + \cos(\alpha))}{2 \cdot AH^2}.
\)
Ответы: выше по пунктам.
Дано, что пирамида \(ABCDK\) имеет квадратное основание \(ABCD\) со стороной \(m\), вершина \(K\) соединена с вершинами квадрата, а высота пирамиды \(KO\) перпендикулярна плоскости квадрата. Угол между двумя смежными рёбрами пирамиды, выходящими из вершины \(K\), равен \(\alpha\). Требуется найти длины \(KO\), \(KA\), угол \(\angle OEK\), а также \(\cos(\angle CBAK)\).
Диагональ квадрата \(ABCD\) равна \(m \cdot \sqrt{2}\). Так как центр квадрата \(O\) делит диагональ пополам, радиус окружности, описанной вокруг квадрата, равен \(R = \frac{m \cdot \sqrt{2}}{2}\).
Обозначим \(OK = x\), \(AK = y\). Рассмотрим прямоугольный треугольник \(\triangle AOK\), где гипотенуза \(AK = y\), катеты \(OA = \frac{m \cdot \sqrt{2}}{2}\) и \(OK = x\). По теореме Пифагора:
\(
\left(\frac{m \cdot \sqrt{2}}{2}\right)^2 + x^2 = y^2.
\)
После упрощения:
\(
\frac{m^2}{2} + x^2 = y^2 \tag{1}.
\)
Теперь применим теорему косинусов для треугольника \(\triangle AKB\), где стороны \(AK = y\), \(BK = y\), а сторона \(AB = m\):
\(
m^2 = y^2 + y^2 — 2 \cdot y \cdot y \cdot \cos(\alpha).
\)
Упростим:
\(
m^2 = 2 \cdot y^2 \cdot (1 — \cos(\alpha)).
\)
Отсюда:
\(
\cos(\alpha) = 1 — \frac{m^2}{2 \cdot y^2} \tag{2}.
\)
Подставляем выражение для \(\cos(\alpha)\) из (2) в уравнение (1):
\(
x^2 = y^2 — \frac{m^2}{2}.
\)
Из (2) выразим \(y^2\):
\(
y^2 = \frac{m^2}{2 \cdot (1 — \cos(\alpha))}.
\)
Подставляем это в уравнение для \(x^2\):
\(
x^2 = \frac{m^2}{2 \cdot (1 — \cos(\alpha))} — \frac{m^2}{2}.
\)
Приводим к общему знаменателю:
\(
x^2 = \frac{m^2}{2} \cdot \left(\frac{1}{1 — \cos(\alpha)} — 1\right).
\)
Упрощаем:
\(
x^2 = \frac{m^2}{2} \cdot \frac{\cos(\alpha)}{1 — \cos(\alpha)}.
\)
Или:
\(
x^2 = \frac{m^2 \cdot \cos(\alpha)}{2 \cdot (1 — \cos(\alpha))}.
\)
Берём корень:
\(
x = \frac{m}{\sqrt{2 \cdot (1 — \cos(\alpha))}}.
\)
Теперь найдём \(y\):
\(
y = \sqrt{\frac{m^2}{2 \cdot (1 — \cos(\alpha))}} = \frac{m}{\sqrt{1 — \cos(\alpha)}}.
\)
Для определения угла \(\angle OEK\) найдём тангенс:
\(
\tan(\angle OEK) = \frac{2 \cdot x}{m}.
\)
Подставляя \(x\):
\(
\tan(\angle OEK) = \frac{2 \cdot \frac{m}{\sqrt{2 \cdot (1 — \cos(\alpha))}}}{m}.
\)
Упрощаем:
\(
\tan(\angle OEK) = \frac{2}{\sqrt{2 \cdot (1 — \cos(\alpha))}}.
\)
Найдём \(\cos(\angle CBAK)\) через теорему косинусов для \(\triangle CHA\), где \(CH = HA = AH\):
\(
\cos(\angle CBAK) = 1 — \frac{m^2 \cdot (1 + \cos(\alpha))}{2 \cdot AH^2}.
\)
Здесь \(AH^2 = m^2 — z^2\), где \(z^2 = \frac{m^2 \cdot (1 + \cos(\alpha))}{4}\).
Подставляем и упрощаем:
\(
AH^2 = m^2 — \frac{m^2 \cdot (1 + \cos(\alpha))}{4}.
\)
\(
AH^2 = \frac{m^2 \cdot (3 — \cos(\alpha))}{4}.
\)
Теперь подставляем в формулу для \(\cos(\angle CBAK)\):
\(
\cos(\angle CBAK) = 1 — \frac{m^2 \cdot (1 + \cos(\alpha))}{2 \cdot \frac{m^2 \cdot (3 — \cos(\alpha))}{4}}.
\)
Упрощаем:
\(
\cos(\angle CBAK) = 1 — \frac{2 \cdot (1 + \cos(\alpha))}{3 — \cos(\alpha)}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!