
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 255 Атанасян — Подробные Ответы
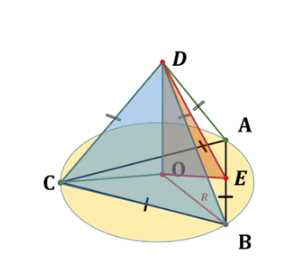
В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен \(\varphi\). Найдите высоту этой пирамиды.
Дано:
\(
ABCD — \text{пирамида}, \quad ABC — \text{треугольник}, \quad AB = BC = CA = 8, \)
\(\quad DO \perp ABC, \quad DA = DB = DC, \quad \angle CDB = \varphi.
\)
Найти: \(DO = H\).
Решение:
Используем результат задачи:
\(
\cos(\angle CDB) = \frac{6 \cdot H^2 — 64}{6 \cdot H^2 + 128}.
\)
Умножим обе части на \((6 \cdot H^2 + 128)\):
\(
\cos(\varphi) \cdot (6 \cdot H^2 + 128) = 6 \cdot H^2 — 64.
\)
Раскрываем скобки:
\(
\cos(\varphi) \cdot 6 \cdot H^2 + 64 \cdot \cos(\varphi) = 6 \cdot H^2 — 64.
\)
Собираем подобные члены:
\(
3 \cdot H^2 \cdot (\cos(\varphi) — 1) = -32 — 64 \cdot \cos(\varphi).
\)
Выражаем \(H^2\):
\(
H^2 = \frac{32(1 + 2 \cdot \cos(\varphi))}{3(1 — \cos(\varphi))}.
\)
Берем корень:
\(
H = 4 \cdot \sqrt{\frac{2 + 4 \cdot \cos(\varphi)}{3 — 3 \cdot \cos(\varphi)}}.
\)
Ответ:
\(
H = 4 \cdot \sqrt{\frac{2 + 4 \cdot \cos(\varphi)}{3 — 3 \cdot \cos(\varphi)}}.
\)
Дано, что пирамида \(ABCD\) имеет в основании равносторонний треугольник \(ABC\), у которого \(AB = BC = CA = 8\). Высота пирамиды \(DO\) перпендикулярна плоскости основания \(ABC\), а боковые ребра \(DA = DB = DC\) равны между собой. Угол между ребрами \(DC\) и \(DB\) обозначен как \(\angle CDB = \varphi\). Требуется найти высоту \(DO = H\).
Для решения используем известную формулу для косинуса угла \(\angle CDB\):
\(
\cos(\angle CDB) = \frac{6 \cdot H^2 — 64}{6 \cdot H^2 + 128}.
\)
Умножаем обе части уравнения на знаменатель \(6 \cdot H^2 + 128\), чтобы избавиться от дроби:
\(
\cos(\varphi) \cdot (6 \cdot H^2 + 128) = 6 \cdot H^2 — 64.
\)
Раскрываем скобки в левой части уравнения:
\(
6 \cdot H^2 \cdot \cos(\varphi) + 128 \cdot \cos(\varphi) = 6 \cdot H^2 — 64.
\)
Переносим все члены, содержащие \(H^2\), в одну часть уравнения, а остальные — в другую:
\(
6 \cdot H^2 — 6 \cdot H^2 \cdot \cos(\varphi) = -64 — 128 \cdot \cos(\varphi).
\)
В левой части выносим \(6 \cdot H^2\) за скобки:
\(
6 \cdot H^2 \cdot (1 — \cos(\varphi)) = -64 — 128 \cdot \cos(\varphi).
\)
Делим обе части уравнения на 6:
\(
H^2 \cdot (1 — \cos(\varphi)) = \frac{-64 — 128 \cdot \cos(\varphi)}{6}.
\)
Приводим правую часть к общему знаменателю:
\(
H^2 \cdot (1 — \cos(\varphi)) = \frac{-32(1 + 2 \cdot \cos(\varphi))}{3}.
\)
Выражаем \(H^2\), разделив обе части на \((1 — \cos(\varphi))\):
\(
H^2 = \frac{32(1 + 2 \cdot \cos(\varphi))}{3(1 — \cos(\varphi))}.
\)
Теперь берем квадратный корень из обеих частей:
\(
H = \sqrt{\frac{32(1 + 2 \cdot \cos(\varphi))}{3(1 — \cos(\varphi))}}.
\)
Упрощаем выражение, вынося множитель 4:
\(
H = 4 \cdot \sqrt{\frac{2 + 4 \cdot \cos(\varphi)}{3 — 3 \cdot \cos(\varphi)}}.
\)
Таким образом, высота пирамиды \(DO\) равна:
\(
H = 4 \cdot \sqrt{\frac{2 + 4 \cdot \cos(\varphi)}{3 — 3 \cdot \cos(\varphi)}}.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!