
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 254 Атанасян — Подробные Ответы
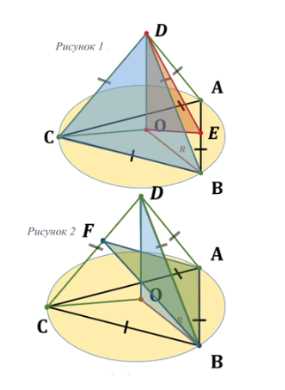
В правильной треугольной пирамиде сторона основания равна \(a\), высота равна \(H\). Найдите:
а) боковое ребро пирамиды;
б) плоский угол при вершине пирамиды;
в) угол между боковым ребром и плоскостью основания пирамиды;
г) угол между боковой гранью и основанием пирамиды;
д) двугранный угол при боковом ребре пирамиды.
Дано: пирамида \(ABCD\), основание — равносторонний треугольник со стороной \(a\), высота пирамиды \(DO = H\). Найти длины рёбер и углы.
Длина \(DA = DB = DC\) находится по теореме Пифагора:
\(
DB = \sqrt{DO^2 + BO^2} = \sqrt{H^2 + \frac{a^2}{3}}
\)
Угол \(\angle DBO\):
\(
\tan(\angle DBO) = \frac{DO}{BO} = \frac{H}{\frac{a}{\sqrt{3}}} = \frac{\sqrt{3} \cdot H}{a}
\)
Угол \(\angle CDB\) по теореме косинусов:
\(
\cos(\angle CDB) = \frac{BD^2 + CD^2 — BC^2}{2 \cdot BD \cdot CD}
\)
Подставляем:
\(
\cos(\angle CDB) = \frac{2 \cdot \left(H^2 + \frac{a^2}{3}\right) — a^2}{2 \cdot \left(H^2 + \frac{a^2}{3}\right)} = \frac{6H^2 — a^2}{6H^2 + 2a^2}
\)
Угол \(\angle DEO\):
\(
\tan(\angle DEO) = \frac{DO}{OE}, \, OE = \frac{a}{2\sqrt{3}} \quad \Rightarrow \quad \tan(\angle DEO) = \frac{2\sqrt{3} \cdot H}{a}
\)
Угол \(\angle AFB\) по теореме косинусов:
\(
\cos(\angle AFB) = \frac{2 \cdot FB^2 — AB^2}{2 \cdot FB^2}, \, FB^2 = a^2 \cdot \frac{12H^2 + a^2}{12H^2 + 4a^2}
\)
Подставляем:
\(
\cos(\angle AFB) = 1 — \frac{6H^2 — a^2}{12H^2 + 4a^2}
\)
Рассмотрим пирамиду \(ABCD\), где основанием является равносторонний треугольник \(ABC\) со стороной \(a\), а высота пирамиды \(DO = H\). Все боковые рёбра пирамиды равны между собой, то есть \(DA = DB = DC\). Для решения задачи нам нужно найти длины рёбер и углы, указанные в условии.
Сначала найдем длину бокового ребра \(DB\). Для этого используем теорему Пифагора в прямоугольном треугольнике \(DOB\), где \(DO = H\) — высота пирамиды, а \(BO\) — расстояние от центра описанной окружности треугольника \(ABC\) до вершины \(B\). Радиус описанной окружности равностороннего треугольника \(ABC\) равен \(\frac{a}{\sqrt{3}}\). Тогда:
\(
DB = \sqrt{DO^2 + BO^2} = \sqrt{H^2 + \left(\frac{a}{\sqrt{3}}\right)^2} = \sqrt{H^2 + \frac{a^2}{3}}
\)
Теперь найдем угол \(\angle DBO\). Для этого используем определение тангенса угла:
\(
\tan(\angle DBO) = \frac{DO}{BO}
\)
Подставляем значения \(DO = H\) и \(BO = \frac{a}{\sqrt{3}}\):
\(
\tan(\angle DBO) = \frac{H}{\frac{a}{\sqrt{3}}} = \frac{\sqrt{3} \cdot H}{a}
\)
Для нахождения угла \(\angle CDB\) воспользуемся теоремой косинусов в треугольнике \(CDB\). Согласно теореме косинусов:
\(
BC^2 = BD^2 + CD^2 — 2 \cdot BD \cdot CD \cdot \cos(\angle CDB)
\)
Так как \(BD = CD = \sqrt{H^2 + \frac{a^2}{3}}\) и \(BC = a\), подставляем значения:
\(
a^2 = 2 \cdot \left(H^2 + \frac{a^2}{3}\right) — 2 \cdot \left(H^2 + \frac{a^2}{3}\right) \cdot \cos(\angle CDB)
\)
Выражаем \(\cos(\angle CDB)\):
\(
\cos(\angle CDB) = \frac{2 \cdot \left(H^2 + \frac{a^2}{3}\right) — a^2}{2 \cdot \left(H^2 + \frac{a^2}{3}\right)} = \frac{6H^2 — a^2}{6H^2 + 2a^2}
\)
Теперь найдем угол \(\angle DEO\). Для этого используем определение тангенса угла:
\(
\tan(\angle DEO) = \frac{DO}{OE}
\)
Здесь \(OE\) — радиус вписанной окружности треугольника \(ABC\), который равен \(\frac{a}{2\sqrt{3}}\). Тогда:
\(
\tan(\angle DEO) = \frac{H}{\frac{a}{2\sqrt{3}}} = \frac{2\sqrt{3} \cdot H}{a}
\)
Для нахождения угла \(\angle AFB\) сначала найдем длину \(FB\). Используем теорему Пифагора в треугольнике \(CFB\), где \(CB = a\) и \(CF = x\). Обозначим \(CF = x\), тогда:
\(
CB^2 = CF^2 + FB^2
\)
Выражаем \(FB^2\):
\(
FB^2 = CB^2 — CF^2
\)
Подставляем значения \(CB = a\) и \(CF = \frac{a^2}{2\sqrt{H^2 + \frac{a^2}{3}}}\) и решаем для \(FB^2\):
\(
FB^2 = a^2 — \left(\frac{a^2}{2\sqrt{H^2 + \frac{a^2}{3}}}\right)^2
\)
После упрощений получаем:
\(
FB^2 = a^2 \cdot \frac{12H^2 + a^2}{12H^2 + 4a^2}
\)
Теперь используем теорему косинусов для треугольника \(ABF\), где \(AB = a\), \(AF = FB\):
\(
\cos(\angle AFB) = \frac{2 \cdot FB^2 — AB^2}{2 \cdot FB^2}
\)
Подставляем найденное значение \(FB^2\):
\(
\cos(\angle AFB) = 1 — \frac{6H^2 — a^2}{12H^2 + 4a^2}
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!