
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 253 Атанасян — Подробные Ответы
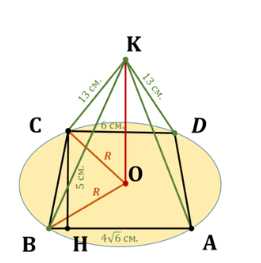
Основанием пирамиды является равнобедренная трапеция с основаниями 6 см и \(4 \frac{6}{6} \, \text{см}\) и высотой 5 см. Каждое боковое ребро пирамиды равно 13 см. Найдите её высоту
Дано:
\(ABCDK\) — пирамида, \(ABCD\) — трапеция, \(BC = AD\), \(AB \parallel CD\), \(AB = 4\sqrt{6} \, \text{см}, CD = 6 \, \text{см}, CH \perp CD, CH = 5 \, \text{см}, KO \perp ABCD\), \(KC = KA = 13 \, \text{см}, KD = KB = 13 \, \text{см}\).
Найти: \(OK\).
Решение:
Основание \(ABCD\) — равнобедренная трапеция:
\(
BH = \frac{AB — CD}{2} = 2\sqrt{6} — 3 \, \text{см}, \quad AH = 3 + 2\sqrt{6} \, \text{см}.
\)
По теореме Пифагора в \(\triangle CHB\):
\(
CB = \sqrt{BH^2 + CH^2} = \sqrt{(2\sqrt{6} — 3)^2 + 25} = 3\sqrt{6} — 2 \, \text{см}.
\)
По теореме Пифагора в \(\triangle CHA\):
\(
CA = \sqrt{AH^2 + CH^2} = \sqrt{(2\sqrt{6} + 3)^2 + 25} = 3\sqrt{6} + 2 \, \text{см}.
\)
Используем формулу для радиуса описанной окружности:
\(
R = \frac{AB \cdot BC \cdot AC}{4 \cdot S_{\triangle ABC}}, \quad S_{\triangle ABC} = \frac{1}{2} \cdot AB \cdot CH.
\)
Подставляя значения:
\(
R = \frac{(4\sqrt{6}) \cdot (3\sqrt{6} — 2) \cdot (3\sqrt{6} + 2)}{2 \cdot (4\sqrt{6}) \cdot 5} = 5 \, \text{см}.
\)
По теореме Пифагора в \(\triangle KOA\):
\(
KO = \sqrt{KA^2 — R^2} = \sqrt{169 — 25} = \sqrt{144} = 12 \, \text{см}.
\)
Ответ: \(OK = 12 \, \text{см}\).
Дано, что \(ABCDK\) — пирамида, а \(ABCD\) — равнобедренная трапеция, у которой \(BC = AD\), \(AB \parallel CD\). Известно, что \(AB = 4\sqrt{6}\), \(CD = 6\), \(CH \perp CD\) и \(CH = 5\). Также известно, что \(KC = KA = 13\), \(KD = KB = 13\) и \(KO \perp ABCD\). Требуется найти длину \(OK\).
Начнем с анализа основания \(ABCD\). Так как \(ABCD\) — равнобедренная трапеция, высота, опущенная из вершины \(C\) на основание \(CD\), делит трапецию на два равных прямоугольных треугольника. Найдем отрезок \(BH\), который является частью основания \(AB\), на которую приходится разность длин \(AB\) и \(CD\), деленная на два:
\(BH = \frac{AB — CD}{2} = \frac{4\sqrt{6} — 6}{2} = 2\sqrt{6} — 3\).
Тогда оставшаяся часть основания \(AB\) равна
\(AH = AB — BH = 4\sqrt{6} — (2\sqrt{6} — 3) = 3 + 2\sqrt{6}\).
Далее найдем длину боковой стороны трапеции \(CB\) с использованием теоремы Пифагора в треугольнике \(\triangle CHB\):
\(CB = \sqrt{BH^2 + CH^2} = \sqrt{(2\sqrt{6} — 3)^2 + 5^2}\).
Раскроем квадрат разности:
\((2\sqrt{6} — 3)^2 = (2\sqrt{6})^2 — 2 \cdot 2\sqrt{6} \cdot 3 + 3^2 = 24 — 12\sqrt{6} + 9 = 33 — 12\sqrt{6}\).
Добавим \(CH^2 = 25\):
\(CB = \sqrt{33 — 12\sqrt{6} + 25} = \sqrt{58 — 12\sqrt{6}}\).
Приведем подкоренное выражение:
\(58 — 12\sqrt{6} = (3\sqrt{6})^2 — 2 \cdot 3\sqrt{6} \cdot 2 + 2^2 = (3\sqrt{6} — 2)^2\).
Таким образом, \(CB = 3\sqrt{6} — 2\).
Аналогично находим длину второй боковой стороны трапеции \(CA\) с использованием теоремы Пифагора в треугольнике \(\triangle CHA\):
\(CA = \sqrt{AH^2 + CH^2} = \sqrt{(3 + 2\sqrt{6})^2 + 5^2}\).
Раскроем квадрат суммы:
\((3 + 2\sqrt{6})^2 = 3^2 + 2 \cdot 3 \cdot 2\sqrt{6} + (2\sqrt{6})^2 = 9 + 12\sqrt{6} + 24 = 33 + 12\sqrt{6}\).
Добавим \(CH^2 = 25\):
\(CA = \sqrt{33 + 12\sqrt{6} + 25} = \sqrt{58 + 12\sqrt{6}}\).
Приведем подкоренное выражение:
\(58 + 12\sqrt{6} = (3\sqrt{6})^2 + 2 \cdot 3\sqrt{6} \cdot 2 + 2^2 = (3\sqrt{6} + 2)^2\).
Таким образом, \(CA = 3\sqrt{6} + 2\).
Теперь найдем радиус \(R\) описанной окружности треугольника \(\triangle ABC\). Для этого используем формулу:
\(R = \frac{AB \cdot BC \cdot AC}{4 \cdot S_{\triangle ABC}}\),
где площадь треугольника \(S_{\triangle ABC}\) равна
\(S_{\triangle ABC} = \frac{1}{2} \cdot AB \cdot CH = \frac{1}{2} \cdot 4\sqrt{6} \cdot 5 = 10\sqrt{6}\).
Подставим значения:
\(R = \frac{(4\sqrt{6}) \cdot (3\sqrt{6} — 2) \cdot (3\sqrt{6} + 2)}{4 \cdot 10\sqrt{6}}\).
Раскроем произведение \((3\sqrt{6} — 2) \cdot (3\sqrt{6} + 2)\):
\((3\sqrt{6})^2 — 2^2 = 54 — 4 = 50\).
Тогда:
\(R = \frac{4\sqrt{6} \cdot 50}{4 \cdot 10\sqrt{6}} = 5\).
Наконец, найдем длину \(KO\) с использованием теоремы Пифагора в треугольнике \(\triangle KOA\):
\(KO = \sqrt{KA^2 — R^2} = \sqrt{13^2 — 5^2} = \sqrt{169 — 25} = \sqrt{144} = 12\).
Ответ: \(OK = 12 \, \text{см}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!