
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 251 Атанасян — Подробные Ответы
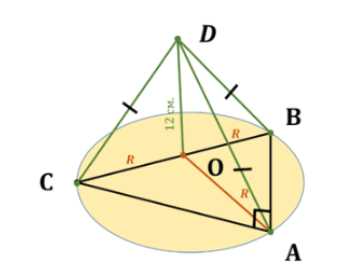
Основанием пирамиды \(DABC\) является прямоугольный треугольник с гипотенузой \(BC\). Боковые рёбра пирамиды равны друг другу, а её высота равна 12 см. Найдите боковое ребро пирамиды, если \(BC = 10 \, \text{см}\).
Дано:
Пирамида \(ABCD\), \(\triangle ABC\) прямоугольный (\(\angle BAC = 90^\circ\)), \(BC = 10 \, \text{см}\), \(DO \perp ABCD\), \(OD = 12 \, \text{см}\), \(DC = DA = DB\).
Найти: \(AD\).
Решение:
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, следовательно, радиус окружности \(R = 5 \, \text{см}\).
По теореме Пифагора для \(\triangle AOD\) находим:
\(
DA = \sqrt{AO^2 + DO^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \, \text{см}.
\)
Ответ: \(DC = DA = DB = 13 \, \text{см}\).
Дано, что \(\triangle ABC\) является прямоугольным, где \(\angle BAC = 90^\circ\). В прямоугольном треугольнике центр описанной окружности всегда лежит на середине гипотенузы. Гипотенузой в данном случае является отрезок \(BC\), длина которого равна \(10 \, \text{см}\). Следовательно, радиус описанной окружности равен половине длины гипотенузы: \(R = \frac{BC}{2} = \frac{10}{2} = 5 \, \text{см}\).
Обозначим точку \(O\) как центр окружности, описанной вокруг \(\triangle ABC\). Тогда \(O\) лежит на середине гипотенузы \(BC\), и расстояние от точки \(O\) до вершины \(A\) равно радиусу \(R\). Таким образом, \(AO = R = 5 \, \text{см}\).
По условию, высота пирамиды \(DO\) перпендикулярна плоскости основания \(ABCD\) и равна \(12 \, \text{см}\). Теперь рассмотрим прямоугольный треугольник \(\triangle AOD\), где \(AO = 5 \, \text{см}\), \(DO = 12 \, \text{см}\), а \(DA\) является гипотенузой. Для нахождения \(DA\) воспользуемся теоремой Пифагора:
\(
DA = \sqrt{AO^2 + DO^2}
\)
Подставляем известные значения:
\(
DA = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \, \text{см}
\)
Так как пирамида симметрична, то \(DC = DA = DB = 13 \, \text{см}\).
Ответ: \(DC = DA = DB = 13 \, \text{см}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!