
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 249 Атанасян — Подробные Ответы
В пирамиде все боковые рёбра равны между собой. Докажите, что:
а) высота пирамиды проходит через центр окружности, описанной около основания;
б) все боковые рёбра пирамиды составляют равные углы с плоскостью основания.
Дано: Пирамида, боковые ребра равны.
Доказать:
а) Высота проходит через центр описанной окружности.
б) Боковые ребра составляют с основанием равные углы.
Решение:
Так как решение не зависит от количества вершин в основании пирамиды, для простоты возьмем \(n = 3\).
Обозначим \(DO\) как высоту пирамиды.
По построению имеем три равных прямоугольных треугольника:
\(\triangle AOD = \triangle BOD = \triangle COD\) (по гипотенузе и катету).
а) \(AO = BO = CO\), следовательно, \(O\) — центр вписанной окружности. Доказано.
б) \(\angle DAO = \angle DBO = \angle DCO\). Доказано.
Ответ: Что и требовалось доказать.
Дано: Пирамида с равными боковыми ребрами. Необходимо доказать два утверждения: высота пирамиды проходит через центр описанной окружности основания, а также, что боковые ребра составляют с основанием равные углы.
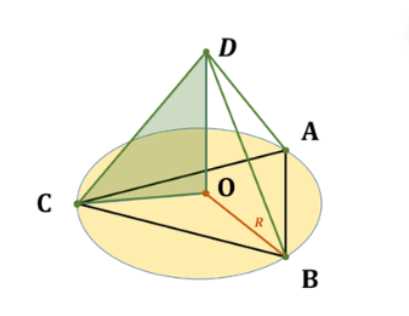
Рассмотрим пирамиду, основание которой представляет собой правильный многоугольник. Для простоты чертежа возьмем случай, когда основание является правильным треугольником (n = 3). Пусть \( DO \) — это высота пирамиды, которая перпендикулярна плоскости основания и проходит через центр основания \( O \).
В основании пирамиды лежит правильный треугольник \( ABC \). Его центр \( O \) является одновременно центром описанной окружности треугольника \( ABC \). Боковые ребра \( DA, DB, DC \) равны по условию.
Рассмотрим треугольники \( \triangle AOD, \triangle BOD \) и \( \triangle COD \). Все они являются прямоугольными, так как \( DO \) — высота пирамиды, перпендикулярная основанию. Кроме того, в каждом из этих треугольников гипотенуза равна длине бокового ребра, а один из катетов (общий для всех треугольников) равен радиусу описанной окружности основания.
Из равенства гипотенузы и одного катета следует, что треугольники \( \triangle AOD, \triangle BOD \) и \( \triangle COD \) равны по гипотенузе и катету. Это доказывает, что углы между высотой пирамиды и боковыми ребрами равны:
\(
\angle DAO = \angle DBO = \angle DCO
\)
Так как точки \( A, B, C \) равноудалены от точки \( O \) (\( AO = BO = CO \)), то \( O \) является центром описанной окружности основания. Высота пирамиды \( DO \), проходящая через \( O \), подтверждает это.
Таким образом, доказано, что высота проходит через центр описанной окружности основания и что боковые ребра составляют с основанием равные углы.
Ответ: что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!