Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 247 Атанасян — Подробные Ответы
Двугранные углы при основании пирамиды равны. Докажите, что:
а) высота пирамиды проходит через центр окружности, вписанной в основание пирамиды;
б) высоты всех боковых граней, проведённые из вершины пирамиды, равны;
в) площадь боковой поверхности пирамиды равна половине произведения периметра основания на высоту боковой грани, проведённую из вершины пирамиды.
Дано: пирамида с равными двугранными углами при основании.
Доказать:
а) высота проходит через центр вписанной окружности.
б) высоты граней равны.
в) \(S_{\text{бок}} = \frac{1}{2} \cdot P_{\text{пирамиды}} \cdot h_{\text{грани}}\).
Решение:
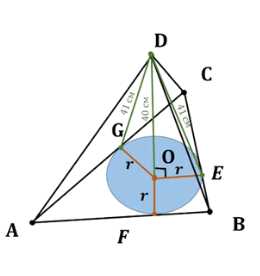
Так как решение не зависит от количества вершин в основании пирамиды, рассмотрим пример. Пусть \(DO\) — высота пирамиды, \(DE, DF, DG\) — высоты граней.
По теореме о трёх перпендикулярах: \(EO \perp BC, FO \perp AB, GO \perp AC\).
По построению:
\(\triangle EOD = \triangle GOD = \triangle FOD\) (по углу и катету).
Следовательно:
1) \(EO = FO = GO\), а \(O\) — центр вписанной окружности (доказано для пункта а).
2) \(ED = FD = GD\) (доказано для пункта б).
Для любого количества граней:
\(
S_{\text{бок}} = \sum \frac{1}{2} \cdot l_{\text{грани}} \cdot h_{\text{грани}} = \frac{1}{2} \cdot P_{\text{пирамиды}} \cdot h_{\text{грани}}.
\)
Ответ: что и требовалось доказать.
Дано: пирамида с равными двугранными углами при основании. Требуется доказать три утверждения: высота пирамиды проходит через центр вписанной окружности, высоты граней равны, а боковая поверхность выражается как половина произведения периметра основания на высоту грани.
Для доказательства рассмотрим пирамиду с основанием, имеющим произвольное количество вершин. В качестве примера выберем треугольное основание, так как рассуждения остаются аналогичными для любого числа сторон.
Обозначим \(DO\) как высоту пирамиды, а \(DE, DF, DG\) как высоты граней. Центр вписанной окружности обозначим как \(O\).
Применим теорему о трех перпендикулярах. Согласно этой теореме, если прямая перпендикулярна плоскости, то она также будет перпендикулярна любой прямой, лежащей в этой плоскости. В нашем случае высота пирамиды \(DO\) перпендикулярна плоскости основания, а значит, она также перпендикулярна сторонам основания \(BC, AB, AC\). Это дает нам следующие перпендикуляры: \(EO \perp BC\), \(FO \perp AB\), \(GO \perp AC\).
Рассмотрим три прямоугольных треугольника: \(\triangle EOD, \triangle GOD, \triangle FOD\). Эти треугольники равны между собой, так как у них равны один острый угол и прилежащий катет. Следовательно, гипотенузы \(EO, FO, GO\) также равны. Это означает, что точка \(O\) является центром вписанной окружности основания. Таким образом, доказано первое утверждение.
Перейдем к высотам граней. Из равенства треугольников следует, что \(ED = FD = GD\). Все высоты граней равны. Это доказывает второе утверждение.
Для доказательства третьего утверждения найдем площадь боковой поверхности пирамиды. Каждая грань пирамиды имеет площадь, равную половине произведения длины стороны основания на высоту грани. Суммируя площади всех граней, получаем:
\(
S_{\text{бок}} = \frac{1}{2} \cdot l_{\text{грани}_1} \cdot h_{\text{грани}_1} + \frac{1}{2} \cdot l_{\text{грани}_2} \cdot h_{\text{грани}_2} + \ldots
\)
Так как высоты граней равны (\(h_{\text{грани}_1} = h_{\text{грани}_2} = \ldots = h_{\text{грани}}\)), можно вынести \(h_{\text{грани}}\) за скобки:
\(
S_{\text{бок}} = \frac{1}{2} \cdot h_{\text{грани}} \cdot (l_{\text{грани}_1} + l_{\text{грани}_2} + \ldots)
\)
Сумма длин сторон основания равна периметру основания (\(P_{\text{пирамиды}}\)). Таким образом, получаем:
\(
S_{\text{бок}} = \frac{1}{2} \cdot P_{\text{пирамиды}} \cdot h_{\text{грани}}
\)
Это доказывает третье утверждение.
Ответ: что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.