ГДЗ по Геометрии 10 класс Номер 246 Атанасян — Подробные Ответы

Высота треугольной пирамиды равна 40 см, а высота каждой боковой грани, проведённая из вершины пирамиды, равна 41 см.
а) Докажите, что высота пирамиды проходит через центр окружности, вписанной в её основание.
б) Найдите площадь основания пирамиды, если его периметр равен 42 см.

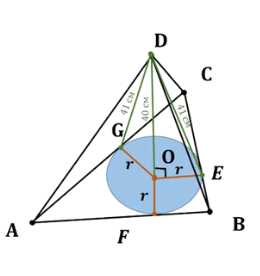
Дано: пирамида \(ABCD\), \(ABC\) — треугольник, \(DG = DE = DF = 41 \, \text{см}\), \(DO \perp ABCD\), \(DO = 40 \, \text{см}\), \(P_{ABC} = 42\). Доказать: \(O\) — центр вписанной окружности \(\triangle ABC\). Найти: \(S_{\text{основания}}\).

По построению: \(\triangle EOD = \triangle GOD = \triangle FOD\) (по гипотенузе и катету), следовательно, \(EO = FO = GO\). По теореме о трёх перпендикулярах \(EO \perp BC\), \(FO \perp AB\), \(GO \perp AC\), значит, \(O\) — центр вписанной окружности \(\triangle ABC\).

По теореме Пифагора в \(\triangle EOD\):
\(
OE = \sqrt{DE^2 — DO^2} = \sqrt{41^2 — 40^2} = \sqrt{1681 — 1600} = \sqrt{81} = 9 \, \text{см}.
\)

Площадь основания:
\(
S_{\text{основания}} = S_{ABC} = p \cdot r = \frac{P_{ABC} \cdot OE}{2} = \frac{42 \cdot 9}{2} = 189 \, \text{см}^2.
\)

Ответ: \(S_{\text{основания}} = 189 \, \text{см}^2\).

Дано: пирамида \(ABCD\), треугольник \(ABC\), \(DG = DE = DF = 41 \, \text{см}\), \(DO \perp ABCD\), \(DO = 40 \, \text{см}\), \(P_{ABC} = 42\). Требуется доказать, что \(O\) — центр вписанной окружности треугольника \(ABC\), и найти площадь основания \(S_{\text{основания}}\).

Рассмотрим треугольники \(\triangle EOD\), \(\triangle GOD\) и \(\triangle FOD\). Эти треугольники прямоугольные, так как \(DO \perp ABCD\). Кроме того, их гипотенузы равны (\(DE = DG = DF = 41 \, \text{см}\)), а также один из катетов у всех треугольников равен (\(DO = 40 \, \text{см}\)). Таким образом, по гипотенузе и катету (\(DE = DG = DF\) и \(DO\)) треугольники \(\triangle EOD\), \(\triangle GOD\) и \(\triangle FOD\) равны. Следовательно, их вторые катеты равны: \(EO = FO = GO\).

Применим теорему о трёх перпендикулярах. По этой теореме, если \(DO \perp ABCD\), а из точки \(O\) опущены перпендикуляры \(EO \perp BC\), \(FO \perp AB\), \(GO \perp AC\), то точка \(O\) является центром вписанной окружности треугольника \(ABC\). Таким образом, доказано, что \(O\) — центр вписанной окружности треугольника \(ABC\).

Теперь найдём радиус вписанной окружности \(r\), который равен \(EO\). Для этого используем теорему Пифагора в прямоугольном треугольнике \(\triangle EOD\):
\(
EO = \sqrt{DE^2 — DO^2}.
\)
Подставим значения: \(DE = 41 \, \text{см}\), \(DO = 40 \, \text{см}\). Тогда:
\(
EO = \sqrt{41^2 — 40^2} = \sqrt{1681 — 1600} = \sqrt{81} = 9 \, \text{см}.
\)

Теперь найдём площадь треугольника \(ABC\). Формула площади через радиус вписанной окружности:
\(
S_{ABC} = p \cdot r,
\)
где \(p\) — полупериметр треугольника, \(r\) — радиус вписанной окружности. Полупериметр треугольника равен:
\(
p = \frac{P_{ABC}}{2} = \frac{42}{2} = 21 \, \text{см}.
\)
Подставим значения \(p = 21 \, \text{см}\) и \(r = 9 \, \text{см}\) в формулу площади:
\(
S_{ABC} = 21 \cdot 9 = 189 \, \text{см}^2.
\)

Ответ: \(S_{\text{основания}} = 189 \, \text{см}^2\).