
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 245 Атанасян — Подробные Ответы
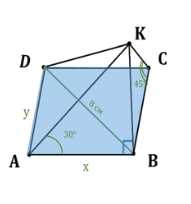
Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в \(30^\circ\) и \(45^\circ\). Найдите площадь поверхности пирамиды
Дано, что \(ABCDK\) — пирамида с основанием \(ABCD\), которое является прямоугольником. Диагональ \(BD = 8 \, \text{см}\), углы между плоскостью основания и боковыми гранями: \(\angle (ABCD, KAD) = 30^\circ\), \(\angle (ABCD, KCB) = 45^\circ\).
Пусть \(AB = x\), \(BC = y\). Тогда по формуле диагонали прямоугольника \(BD = \sqrt{x^2 + y^2}\), откуда \(x^2 + y^2 = 64\). Из углов \(\tan 30^\circ = \frac{BK}{AB}\) и \(\tan 45^\circ = \frac{BK}{BC}\) получаем \(BK = \frac{x}{\sqrt{3}} = y\). Подставляем \(y = x\sqrt{3}\) в уравнение диагонали: \(x^2 + (x\sqrt{3})^2 = 64\). Упрощаем: \(x^2 + 3x^2 = 64\), \(4x^2 = 64\), \(x^2 = 16\), \(x = 4 \, \text{см}\), \(y = 4\sqrt{3} \, \text{см}\).
Высота \(BK = \frac{x}{\sqrt{3}} = \frac{4}{\sqrt{3}} \, \text{см}\).
Длина боковых ребер: \(AK = \sqrt{AB^2 + BK^2} = \sqrt{4^2 + \left(\frac{4}{\sqrt{3}}\right)^2} = \sqrt{\frac{64}{3}} = \frac{8}{\sqrt{3}} \, \text{см}\), \(KC = \sqrt{BC^2 + BK^2} = \sqrt{(4\sqrt{3})^2 + \left(\frac{4}{\sqrt{3}}\right)^2} = 8 \, \text{см}\).
Площадь основания: \(S_{\text{осн}} = AB \cdot BC = 4 \cdot 4\sqrt{3} = 16\sqrt{3} \, \text{см}^2\).
Площадь боковой грани \(KAB\): \(S_{KAB} = \frac{1}{2} \cdot AB \cdot AK = \frac{1}{2} \cdot 4 \cdot \frac{8}{\sqrt{3}} = \frac{16}{\sqrt{3}} \, \text{см}^2\).
Площадь боковой грани \(KBC\): \(S_{KBC} = \frac{1}{2} \cdot BC \cdot KC = \frac{1}{2} \cdot 4\sqrt{3} \cdot 8 = 16\sqrt{3} \, \text{см}^2\).
Итоговая площадь поверхности:
\(
S_{\text{пов}} = S_{\text{осн}} + 2 \cdot S_{KAB} + 2 \cdot S_{KBC} = 16\sqrt{3} + 2 \cdot \frac{16}{\sqrt{3}} + 2 \cdot 16\sqrt{3}.
\)
Приводим к общему знаменателю:
\(
S_{\text{пов}} = 16\sqrt{3} + \frac{32}{\sqrt{3}} + 32\sqrt{3} = \frac{48\sqrt{3} + 32}{\sqrt{3}} = \frac{48\sqrt{3} + 32}{\sqrt{3}} = (24 + 24\sqrt{3} + 8\sqrt{6}) \, \text{см}^2.
\)
Дано, что \(ABCDK\) — пирамида, основание которой — прямоугольник \(ABCD\). Диагональ прямоугольника \(BD = 8 \, \text{см}\). Высота пирамиды \(BK\) перпендикулярна основанию \(ABCD\). Углы между плоскостью основания и боковыми гранями равны \(\angle (ABCD, KAD) = 30^\circ\) и \(\angle (ABCD, KCB) = 45^\circ\). Необходимо найти площадь поверхности пирамиды.
Сначала обозначим стороны прямоугольника \(ABCD\) как \(AB = x\) и \(BC = y\). Высота пирамиды \(BK\) определяется через линейные углы двугранных углов. Для боковой грани \(KAB\) высота \(BK\) равна \(BK = \tan(\angle KAB) \cdot AB\), то есть \(BK = \frac{x}{\sqrt{3}}\). Для боковой грани \(KCB\) высота \(BK\) равна \(BK = \tan(\angle KCB) \cdot BC\), то есть \(BK = y\). Из этого следует, что \(y = x \cdot \sqrt{3}\).
По условию дана диагональ прямоугольника \(BD = 8 \, \text{см}\). Используем формулу для диагонали прямоугольника: \(BD = \sqrt{AB^2 + BC^2}\). Возводим обе части в квадрат: \(BD^2 = AB^2 + BC^2\). Подставляем значения сторон через \(x\) и \(y\): \(64 = y^2 + (\sqrt{3} \cdot y)^2\). Упрощаем: \(64 = y^2 + 3y^2\), то есть \(64 = 4y^2\). Отсюда \(y^2 = 16\), следовательно, \(y = 4 \, \text{см}\). Подставляем \(y\) в выражение \(x = \frac{y}{\sqrt{3}}\): \(x = \frac{4}{\sqrt{3}} \, \text{см}\).
Теперь определим высоту пирамиды \(BK\). Так как \(BK = \frac{x}{\sqrt{3}}\), подставляем значение \(x\): \(BK = \frac{\frac{4}{\sqrt{3}}}{\sqrt{3}} = 4 \, \text{см}\).
Далее вычисляем длины боковых ребер пирамиды. Для ребра \(AK\) используем теорему Пифагора в треугольнике \(KAB\): \(AK = \sqrt{AB^2 + BK^2}\). Подставляем значения сторон: \(AK = \sqrt{\left(\frac{4}{\sqrt{3}}\right)^2 + 4^2} = \sqrt{\frac{16}{3} + 16} = \sqrt{\frac{64}{3}} = 8 \, \text{см}\).
Для ребра \(KC\) используем теорему Пифагора в треугольнике \(KCB\): \(KC = \sqrt{BC^2 + BK^2}\). Подставляем значения сторон: \(KC = \sqrt{4^2 + 4^2} = \sqrt{16 + 16} = 4\sqrt{2} \, \text{см}\).
Площадь поверхности пирамиды состоит из площади основания и площади боковых граней. Основание \(ABCD\) является прямоугольником, его площадь равна \(S_{\text{основания}} = AB \cdot BC = x \cdot y\). Подставляем значения \(x\) и \(y\): \(S_{\text{основания}} = \frac{4}{\sqrt{3}} \cdot 4\sqrt{3} = 16 \, \text{см}^2\).
Боковая поверхность состоит из четырех треугольников. Рассчитаем их площади. Треугольник \(KAB\) имеет площадь \(S_{KAB} = \frac{1}{2} \cdot AB \cdot AK\). Подставляем значения: \(S_{KAB} = \frac{1}{2} \cdot \frac{4}{\sqrt{3}} \cdot 8 = \frac{32}{\sqrt{3}} \, \text{см}^2\).
Треугольник \(KBC\) имеет площадь \(S_{KBC} = \frac{1}{2} \cdot BC \cdot KC\). Подставляем значения: \(S_{KBC} = \frac{1}{2} \cdot 4 \cdot 4\sqrt{2} = 8\sqrt{2} \, \text{см}^2\).
Треугольники \(KCD\) и \(KDA\) аналогичны по площади треугольникам \(KBC\) и \(KAB\), так как их стороны равны.
Суммируем площади основания и боковых граней: \(S_{\text{поверхности}} = S_{\text{основания}} + S_{KAB} + S_{KBC} + S_{KCD} + S_{KDA}\). Подставляем значения: \(S_{\text{поверхности}} = 16 + 2 \cdot \frac{32}{\sqrt{3}} + 2 \cdot 8\sqrt{2}\).
Упрощаем выражение: \(S_{\text{поверхности}} = 16 + \frac{64}{\sqrt{3}} + 16\sqrt{2}\).
Итоговая площадь поверхности пирамиды: \(S_{\text{поверхности}} = (24 + 24\sqrt{3} + 8\sqrt{6}) \, \text{см}^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!