
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 242 Атанасян — Подробные Ответы
Основанием пирамиды является квадрат, одно из боковых рёбер перпендикулярно к плоскости основания. Плоскость боковой грани, не проходящей через высоту пирамиды, наклонена к плоскости основания под углом \(45^\circ\). Наибольшее боковое ребро равно 12 см. Найдите:
а) высоту пирамиды;
б) площадь боковой поверхности пирамиды.
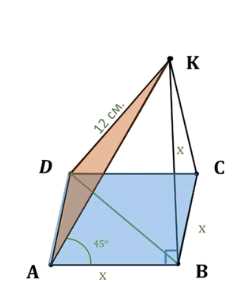
Дано: пирамида \(ABCDK\), основание \(ABCD\) — квадрат со стороной \(x\), \(KD = 12 \, \text{см}\), угол \(\angle (BAD, KAD) = 45^\circ\).
Диагональ квадрата \(BD = \sqrt{2} \cdot x\). Высота пирамиды \(BK = x\). Ребро \(AK = \sqrt{2} \cdot x\). Рассмотрим треугольник \(KDB\), где \(DK^2 = BK^2 + DB^2\):
\(
12^2 = x^2 + (\sqrt{2} \cdot x)^2.
\)
\(
144 = x^2 + 2x^2.
\)
\(
144 = 3x^2.
\)
\(
x^2 = 48, \quad x = 4 \cdot \sqrt{3}.
\)
Высота пирамиды \(h_{ABCDK} = BK = x = 4 \cdot \sqrt{3} \, \text{см}\).
Найдем площадь боковой поверхности. Площадь одного бокового треугольника \(S_{ABK}\):
\(
S_{ABK} = \frac{1}{2} \cdot AB \cdot AK = \frac{1}{2} \cdot x \cdot (\sqrt{2} \cdot x) = \frac{x^2 \cdot \sqrt{2}}{2}.
\)
Общая площадь боковой поверхности:
\(
S_{\text{боковой}} = 4 \cdot S_{ABK} = 4 \cdot \frac{x^2 \cdot \sqrt{2}}{2} = 2 \cdot x^2 \cdot \sqrt{2}.
\)
Подставляем \(x^2 = 48\):
\(
S_{\text{боковой}} = 2 \cdot 48 \cdot \sqrt{2} = 96 \cdot \sqrt{2}.
\)
Представим результат:
\(
S_{\text{боковой}} = 48 \cdot (1 + \sqrt{2}) \, \text{см}^2.
\)
Ответ:
\(
h_{ABCDK} = 4 \cdot \sqrt{3} \, \text{см}, \quad S_{\text{боковой}} = 48 \cdot (1 + \sqrt{2}) \, \text{см}^2.
\)
Дано: пирамида \(ABCDK\), основание \(ABCD\) — квадрат, \(KD = 12 \, \text{см}\), угол \(\angle (BAD, KAD) = 45^\circ\).
Обозначим сторону квадрата за \(x\). Тогда диагональ квадрата \(BD\) равна \(BD = \sqrt{2} \cdot x\), так как диагональ квадрата выражается через его сторону по формуле \(d = a \cdot \sqrt{2}\).
Высота пирамиды \(BK\) перпендикулярна основанию \(ABCD\). Угол между плоскостью \(BAD\) и ребром \(KAD\) равен \(45^\circ\). По условию, \(BK = \tan(45^\circ) \cdot AB\). Так как \(\tan(45^\circ) = 1\), получаем \(BK = AB = x\).
Ребро \(AK\) можно выразить через сторону квадрата \(x\), так как \(AK\) является гипотенузой в прямоугольном треугольнике \(ABK\), где \(AB = x\) и \(BK = x\). По теореме Пифагора:
\(
AK = \sqrt{AB^2 + BK^2} = \sqrt{x^2 + x^2} = \sqrt{2} \cdot x.
\)
Теперь используем треугольник \(KDB\), чтобы найти сторону квадрата \(x\). Этот треугольник прямоугольный, так как \(BK\) — высота пирамиды. По теореме Пифагора:
\(
DK^2 = BK^2 + DB^2.
\)
Подставляем известные данные: \(DK = 12\), \(BK = x\), \(DB = \sqrt{2} \cdot x\). Тогда:
\(
12^2 = x^2 + (\sqrt{2} \cdot x)^2.
\)
Раскрываем скобки:
\(
144 = x^2 + 2x^2.
\)
Складываем:
\(
144 = 3x^2.
\)
Находим \(x^2\):
\(
x^2 = 48.
\)
Берем корень:
\(
x = \sqrt{48} = 4 \cdot \sqrt{3}.
\)
Высота пирамиды \(h_{ABCDK}\) равна \(BK\), а \(BK = x\). Тогда:
\(
h_{ABCDK} = 4 \cdot \sqrt{3} \, \text{см}.
\)
Теперь находим площадь боковой поверхности пирамиды. Площадь боковой поверхности состоит из четырех равнобедренных треугольников \(S_{ABK}\), \(S_{CBK}\), \(S_{CDK}\), \(S_{DAK}\). Рассчитаем площадь одного из треугольников, например, \(S_{ABK}\). Основание треугольника равно \(AB = x\), высота \(AK = \sqrt{2} \cdot x\). Площадь треугольника:
\(
S_{ABK} = \frac{1}{2} \cdot AB \cdot AK = \frac{1}{2} \cdot x \cdot (\sqrt{2} \cdot x) = \frac{x^2 \cdot \sqrt{2}}{2}.
\)
Так как все четыре треугольника равны, общая площадь боковой поверхности:
\(
S_{\text{боковой}} = 4 \cdot S_{ABK} = 4 \cdot \frac{x^2 \cdot \sqrt{2}}{2} = 2 \cdot x^2 \cdot \sqrt{2}.
\)
Подставляем \(x^2 = 48\):
\(
S_{\text{боковой}} = 2 \cdot 48 \cdot \sqrt{2} = 96 \cdot \sqrt{2}.
\)
Представим результат в виде \(S_{\text{боковой}} = 48 \cdot (1 + \sqrt{2}) \, \text{см}^2\), выделив общие множители.
Ответ:
\(
h_{ABCDK} = 4 \cdot \sqrt{3} \, \text{см}, \quad S_{\text{боковой}} = 48 \cdot (1 + \sqrt{2}) \, \text{см}^2.
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!