ГДЗ по Геометрии 10 класс Номер 241 Атанасян — Подробные Ответы

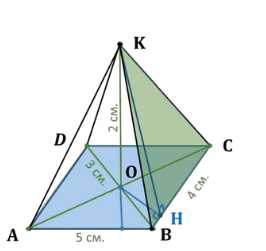
Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь полной поверхности пирамиды

Дано: пирамида \(ABCDK\), основание \(ABCD\) — параллелограмм. Известно, что \(AB = 5\), \(BC = 4\), \(BD = 3\), \(OK = 2\), \(OK \perp ABCD\). Найти полную площадь поверхности пирамиды \(S_{\text{полн}}\).

Площадь основания \(ABCD\) равна \(S_{ABCD} = 12 \, \text{м}^2\), так как \(S_{OBC} = \frac{1}{2} \cdot OB \cdot BC = 3 \, \text{м}^2\), а \(S_{ABCD} = 4 \cdot S_{OBC}\).

Высота \(OH\) в треугольнике \(OBC\) равна \(OH = \frac{2 \cdot S_{OBC}}{BC} = 1.5 \, \text{м}\). По теореме Пифагора \(KH = \sqrt{OK^2 + OH^2} = \sqrt{6.25} = 2.5 \, \text{м}\).

Площадь боковой грани \(KBC\) равна \(S_{KBC} = \frac{1}{2} \cdot KH \cdot BC = 5 \, \text{м}^2\). Аналогично, \(S_{KAD} = 5 \, \text{м}^2\).

Высота \(h_{AOB}\) в треугольнике \(AOB\) равна \(h_{AOB} = \frac{2 \cdot S_{OAB}}{AB} = 1.2 \, \text{м}\). По теореме Пифагора \(h_{AKB} = \sqrt{OK^2 + h_{AOB}^2} = \sqrt{5.44}\).

Площадь грани \(KAB\) равна \(S_{KAB} = \frac{1}{2} \cdot h_{AKB} \cdot AB = \sqrt{34} \, \text{м}^2\). Так как \(S_{KCD} = S_{KAB}\), то \(S_{KCD} = \sqrt{34} \, \text{м}^2\).

Полная площадь поверхности пирамиды равна \(S_{\text{полн}} = S_{ABCD} + S_{KAB} + S_{KBC} + S_{KCD} + S_{KAD} = 22 + 2 \cdot \sqrt{34} \, \text{м}^2\).

Дано: пирамида \(ABCDK\), основание \(ABCD\) — параллелограмм. Известно, что \(AB = 5\), \(BC = 4\), \(BD = 3\), \(OK = 2\), \(OK \perp ABCD\). Необходимо найти полную площадь поверхности пирамиды \(S_{\text{полн}}\).

Рассмотрим основание \(ABCD\). Так как это параллелограмм, то его площадь можно найти через удвоенную площадь одного из треугольников, составляющих этот параллелограмм. Рассмотрим треугольник \(CBD\), который является прямоугольным (по условию). По теореме Пифагора:

\(
S_{OBC} = \frac{1}{2} \cdot OB \cdot BC = \frac{1}{4} \cdot BD \cdot BC = 3 \, \text{м}^2
\)

где \(OB = \frac{BD}{2} = \frac{3}{2}\), так как диагонали параллелограмма делятся пополам.

Площадь всего параллелограмма \(ABCD\) равна:

\(
S_{ABCD} = 4 \cdot S_{OBC} = 12 \, \text{м}^2
\)

Теперь определим высоту \(OH\) в треугольнике \(OBC\). Высота \(OH\) связана с площадью следующим образом:

\(
OH \cdot BC = 2 \cdot S_{OBC}
\)

Отсюда высота \(OH\) находится как:

\(
OH = \frac{2 \cdot S_{OBC}}{BC} = \frac{6}{4} = 1.5 \, \text{м}
\)

Рассмотрим треугольник \(KOH\), который является прямоугольным. Известно, что \(OK = 2\) и \(OH = 1.5\). Найдем \(KH\) по теореме Пифагора:

\(
KH = \sqrt{OK^2 + OH^2} = \sqrt{2^2 + 1.5^2} = \sqrt{4 + 2.25} = \sqrt{6.25} = 2.5 \, \text{м}
\)

Теперь найдем площадь боковой грани \(KBC\). Она равна:

\(
S_{KBC} = \frac{1}{2} \cdot KH \cdot BC = \frac{1}{2} \cdot 2.5 \cdot 4 = 5 \, \text{м}^2
\)

Аналогично, площадь грани \(KAD\) также равна \(5 \, \text{м}^2\), так как \(KAD\) симметрична \(KBC\).

Рассмотрим треугольник \(AOB\). Его площадь равна:

\(
S_{OAB} = \frac{1}{2} \cdot OB \cdot AB = \frac{1}{2} \cdot \frac{3}{2} \cdot 5 = 3 \, \text{м}^2
\)

Высота \(h_{AOB}\) в этом треугольнике находится как:

\(
h_{AOB} = \frac{2 \cdot S_{OAB}}{AB} = \frac{2 \cdot 3}{5} = 1.2 \, \text{м}
\)

Теперь рассмотрим треугольник \(KAB\), который также является прямоугольным. Найдем его высоту \(h_{AKB}\) по теореме Пифагора:

\(
h_{AKB} = \sqrt{OK^2 + h_{AOB}^2} = \sqrt{2^2 + 1.2^2} = \sqrt{4 + 1.44} = \sqrt{5.44}
\)

Площадь грани \(KAB\) равна:

\(
S_{KAB} = \frac{1}{2} \cdot h_{AKB} \cdot AB = \frac{1}{2} \cdot \sqrt{5.44} \cdot 5 = \sqrt{34} \, \text{м}^2
\)

Так как \(KCD\) симметрична \(KAB\), то ее площадь также равна:

\(
S_{KCD} = \sqrt{34} \, \text{м}^2
\)

Полная площадь поверхности пирамиды складывается из площади основания и всех боковых граней:

\(
S_{\text{полн}} = S_{\text{осн}} + S_{\text{бок}} = S_{ABCD} + S_{KAB} + S_{KBC} + S_{KCD} + S_{KAD}
\)

Подставим значения:

\(
S_{\text{полн}} = 12 + \sqrt{34} + 5 + \sqrt{34} + 5 = 22 + 2 \cdot \sqrt{34} \, \text{м}^2
\)

Ответ:

\(
S_{\text{полн}} = 22 + 2 \cdot \sqrt{34} \, \text{м}^2
\)