
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 240 Атанасян — Подробные Ответы
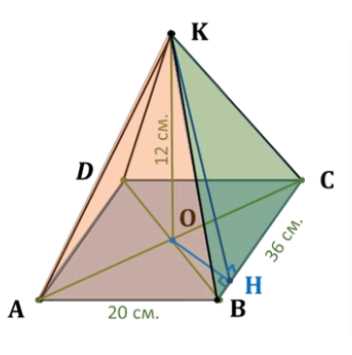
Основанием пирамиды является параллелограмм, стороны которого равны 20 см и 36 см, а площадь равна \(360 \, \text{см}^2\). Высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 см. Найдите площадь боковой поверхности пирамиды.
Дано: пирамида \(ABCDK\), основание \(ABCD\) — параллелограмм. \(AB = 20 \, \text{см}\), \(BC = 36 \, \text{см}\), \(S_{ABCD} = 360 \, \text{см}^2\), \(OK \perp ABCD\), \(OK = 12 \, \text{см}\). Найти: \(S_{\text{бок}}\).
Площадь одной боковой грани, например \(KBC\):
\(
S_{OBC} = \frac{S_{ABCD}}{4} = 90 \, \text{см}^2, \quad OH = \frac{S_{OBC}}{BC} = \frac{90}{36} = 5 \, \text{см}.
\)
Из \(\triangle KON\):
\(
HK = \sqrt{OK^2 + OH^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \, \text{см}.
\)
Площадь \(\triangle KBC\):
\(
S_{KBC} = \frac{1}{2} \cdot KH \cdot BC = \frac{1}{2} \cdot 13 \cdot 36 = 234 \, \text{см}^2.
\)
Аналогично для \(KAB\):
\(
S_{OAB} = \frac{S_{ABCD}}{4} = 90 \, \text{см}^2, \quad h_{AOB} = \frac{S_{OAB}}{AB} = \frac{90}{20} = 9 \, \text{см}.
\)
Из \(\triangle KAB\):
\(
h_{AKB} = \sqrt{OK^2 + h_{AOB}^2} = \sqrt{12^2 + 9^2} = \sqrt{144 + 81} = \sqrt{225} = 15 \, \text{см}.
\)
Площадь \(\triangle KAB\):
\(
S_{KAB} = \frac{1}{2} \cdot h_{AKB} \cdot AB = \frac{1}{2} \cdot 15 \cdot 20 = 150 \, \text{см}^2.
\)
Для граней \(KCD\) и \(KDA\) аналогично:
\(
S_{KCD} = 150 \, \text{см}^2, \quad S_{KDA} = 234 \, \text{см}^2.
\)
Суммарная площадь боковых граней:
\(
S_{\text{бок}} = S_{KAB} + S_{KBC} + S_{KCD} + S_{KDA} = 150 + 234 + 150 + 234 = 768 \, \text{см}^2.
\)
Ответ: \(S_{\text{бок}} = 768 \, \text{см}^2\).
Дано: пирамида \(ABCDK\), основание \(ABCD\) — параллелограмм. Известно, что \(AB = 20 \, \text{см}\), \(BC = 36 \, \text{см}\), \(S_{ABCD} = 360 \, \text{см}^2\), \(OK \perp ABCD\), \(OK = 12 \, \text{см}\). Нужно найти сумму площадей боковых граней \(S_{\text{бок}}\).
Начнем с нахождения площади одной из боковых граней, например \(KBC\). Основание этой грани — треугольник \(KBC\), а его высота \(KH\) опущена из вершины \(K\) перпендикулярно стороне \(BC\).
Сначала найдем площадь проекции треугольника \(KBC\) на плоскость основания \(ABCD\). Площадь проекции \(S_{OBC}\) равна четверти площади основания, так как \(ABCD\) — параллелограмм, а диагонали делят его на четыре равные части. Тогда:
\(
S_{OBC} = \frac{S_{ABCD}}{4} = \frac{360}{4} = 90 \, \text{см}^2
\)
По формуле площади треугольника через основание и высоту:
\(
S_{OBC} = \frac{1}{2} \cdot OH \cdot BC
\)
Отсюда выражаем \(OH\):
\(
OH = \frac{2 \cdot S_{OBC}}{BC} = \frac{2 \cdot 90}{36} = 5 \, \text{см}
\)
Теперь найдем длину высоты \(KH\) треугольника \(KBC\). Рассмотрим прямоугольный треугольник \(KOH\), где \(OK = 12 \, \text{см}\) и \(OH = 5 \, \text{см}\). По теореме Пифагора:
\(
KH = \sqrt{OK^2 + OH^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \, \text{см}
\)
Площадь треугольника \(KBC\) находится по формуле:
\(
S_{KBC} = \frac{1}{2} \cdot KH \cdot BC = \frac{1}{2} \cdot 13 \cdot 36 = 234 \, \text{см}^2
\)
Аналогично найдем площадь треугольника \(KAB\). Основание \(AB = 20 \, \text{см}\), а высота \(h_{AOB}\) опущена из точки \(O\) на сторону \(AB\). Площадь проекции \(S_{OAB}\) равна:
\(
S_{OAB} = \frac{S_{ABCD}}{4} = \frac{360}{4} = 90 \, \text{см}^2
\)
По формуле площади треугольника:
\(
S_{OAB} = \frac{1}{2} \cdot h_{AOB} \cdot AB
\)
Выразим \(h_{AOB}\):
\(
h_{AOB} = \frac{2 \cdot S_{OAB}}{AB} = \frac{2 \cdot 90}{20} = 9 \, \text{см}
\)
Теперь найдем высоту \(h_{AKB}\) треугольника \(KAB\). Рассмотрим прямоугольный треугольник \(KAB\), где \(OK = 12 \, \text{см}\) и \(h_{AOB} = 9 \, \text{см}\). По теореме Пифагора:
\(
h_{AKB} = \sqrt{OK^2 + h_{AOB}^2} = \sqrt{12^2 + 9^2} = \sqrt{144 + 81} = \sqrt{225} = 15 \, \text{см}
\)
Площадь треугольника \(KAB\) находится по формуле:
\(
S_{KAB} = \frac{1}{2} \cdot h_{AKB} \cdot AB = \frac{1}{2} \cdot 15 \cdot 20 = 150 \, \text{см}^2
\)
Аналогично для треугольников \(KCD\) и \(KDA\), их площади равны:
\(
S_{KCD} = S_{KAB} = 150 \, \text{см}^2, \quad S_{KDA} = S_{KBC} = 234 \, \text{см}^2
\)
Суммируем площади всех боковых граней:
\(
S_{\text{бок}} = S_{KAB} + S_{KBC} + S_{KCD} + S_{KDA} = 150 + 234 + 150 + 234 = 768 \, \text{см}^2
\)
Ответ:
\(
S_{\text{бок}} = 768 \, \text{см}^2
\)
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!