ГДЗ по Геометрии 10 класс Номер 239 Атанасян — Подробные Ответы

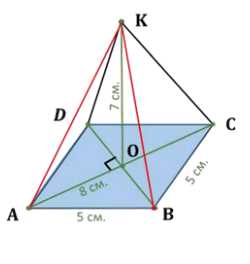
Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если высота её проходит через точку пересечения диагоналей основания и равна 7 см

Дано: \(ABCDK\) — пирамида, \(ABCD\) — ромб, \(AB = 5 \, \text{см}\), \(AC = 8 \, \text{см}\), \(OK \perp ABCD\), \(OK = 7 \, \text{см}\). Найти: \(AK, BK, CK, DK\).

По свойству ромба \(\angle AOB = 90^\circ\), \(AO = OC = \frac{AC}{2} = 4 \, \text{см}\).
По теореме Пифагора из \(\triangle AOB\):
\(
OB = \sqrt{AB^2 — AO^2} = \sqrt{25 — 16} = \sqrt{9} = 3 \, \text{см}.
\)
По теореме Пифагора из \(\triangle AOK\):
\(
AK = \sqrt{OK^2 + AO^2} = \sqrt{49 + 16} = \sqrt{65} \, \text{см}.
\)
По теореме Пифагора из \(\triangle BOK\):
\(
BK = \sqrt{OK^2 + OB^2} = \sqrt{49 + 9} = \sqrt{58} \, \text{см}.
\)

Ответ: \(AK = CK = \sqrt{65} \, \text{см}, \, BK = DK = \sqrt{58} \, \text{см}\).

Дано: \(ABCDK\) — пирамида, \(ABCD\) — ромб. По свойству ромба диагонали пересекаются под прямым углом, то есть \(\angle AOB = 90^\circ\). Также известно, что \(AB = 5 \, \text{см}\), \(AC = 8 \, \text{см}\), \(OK \perp ABCD\), \(OK = 7 \, \text{см}\). Необходимо найти длины отрезков \(AK, BK, CK, DK\).

Сначала вычислим длины отдельных элементов основания ромба. Диагональ \(AC\) делится точкой пересечения диагоналей \(O\) пополам, поэтому \(AO = OC = \frac{AC}{2} = \frac{8}{2} = 4 \, \text{см}\).

Теперь рассмотрим треугольник \(\triangle AOB\). Этот треугольник прямоугольный, так как \(\angle AOB = 90^\circ\). Известны гипотенуза \(AB = 5 \, \text{см}\) и один из катетов \(AO = 4 \, \text{см}\). Найдем второй катет \(OB\) по теореме Пифагора:
\(
OB = \sqrt{AB^2 — AO^2} = \sqrt{5^2 — 4^2} = \sqrt{25 — 16} = \sqrt{9} = 3 \, \text{см}.
\)

Далее рассмотрим треугольник \(\triangle AOK\). Этот треугольник тоже прямоугольный, так как \(OK \perp ABCD\). У него известны катеты \(OK = 7 \, \text{см}\) и \(AO = 4 \, \text{см}\). Найдем гипотенузу \(AK\) по теореме Пифагора:
\(
AK = \sqrt{OK^2 + AO^2} = \sqrt{7^2 + 4^2} = \sqrt{49 + 16} = \sqrt{65} \, \text{см}.
\)

Аналогично рассмотрим треугольник \(\triangle BOK\). Этот треугольник также прямоугольный, у него известны катеты \(OK = 7 \, \text{см}\) и \(OB = 3 \, \text{см}\). Найдем гипотенузу \(BK\) по теореме Пифагора:
\(
BK = \sqrt{OK^2 + OB^2} = \sqrt{7^2 + 3^2} = \sqrt{49 + 9} = \sqrt{58} \, \text{см}.
\)

Так как основание пирамиды \(ABCD\) — ромб, все стороны основания равны, а высота \(OK\) одинакова для всех вершин основания. Следовательно, длины отрезков \(AK\), \(BK\), \(CK\), \(DK\) симметричны. Это значит, что \(AK = CK\) и \(BK = DK\).

Ответ: \(AK = CK = \sqrt{65} \, \text{см}, \, BK = DK = \sqrt{58} \, \text{см}\).