ГДЗ по Геометрии 10 класс Номер 237 Атанасян — Подробные Ответы

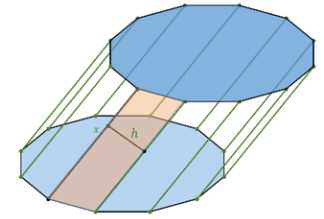
Боковое ребро наклонной четырёхугольной призмы равно 12 см, а перпендикулярным сечением является ромб со стороной 5 см. Найдите площадь боковой поверхности призмы.

Дано:
\(
x = 12 \, \text{см}, \, a = 5 \, \text{см}.
\)
Перпендикулярное сечение — ромб.

Найти:
\(
S_{\text{боковой}} \, ?
\)

Решение:
По формуле:
\(
S_{\text{боковой}} = P \cdot x = (4 \cdot a) \cdot x = (4 \cdot 5) \cdot 12 = 240 \, \text{см}^2.
\)

Ответ:
\(
S_{\text{боковой}} = 240 \, \text{см}^2.
\)

Дано, что наклонная призма имеет боковую грань длиной \(x = 12 \, \text{см}\), а перпендикулярное сечение представляет собой ромб со стороной \(a = 5 \, \text{см}\). Требуется найти площадь боковой поверхности призмы \(S_{\text{боковой}}\).

Для нахождения площади боковой поверхности призмы используется формула:
\(S_{\text{боковой}} = P \cdot x\),
где \(P\) — периметр перпендикулярного сечения, а \(x\) — длина боковой грани.

Поскольку перпендикулярное сечение является ромбом, его периметр \(P\) равен:
\(P = 4 \cdot a\),
где \(a\) — длина стороны ромба. Подставляем значение \(a = 5 \, \text{см}\):
\(P = 4 \cdot 5 = 20 \, \text{см}\).

Теперь подставляем значения \(P = 20 \, \text{см}\) и \(x = 12 \, \text{см}\) в формулу для площади боковой поверхности:
\(S_{\text{боковой}} = P \cdot x = 20 \cdot 12 = 240 \, \text{см}^2\).

Таким образом, площадь боковой поверхности призмы равна \(S_{\text{боковой}} = 240 \, \text{см}^2\).