
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 236 Атанасян — Подробные Ответы
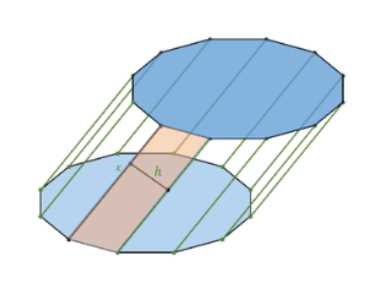
Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро
Дано:
Наклонная призма \(ABC \dots A_1B_1C_1 \dots\),
\(P\) — периметр перпендикулярного сечения,
\(x\) — длина боковой грани.
Доказать:
\(S_{\text{боковой}} = P \cdot x\).
Решение:
Очевидно, что площадь боковой поверхности призмы равна сумме площадей всех боковых граней. Каждая боковая грань является параллелограммом, площадь которого равна произведению длины боковой грани (\(x\)) на высоту (\(h_i\)):
\(
S_{\text{боковой}} = \sum_{i=1}^n S_i = \sum_{i=1}^n (x \cdot h_i) = x \cdot \sum_{i=1}^n h_i
\)
Так как сумма высот всех боковых граней равна периметру перпендикулярного сечения (\(\sum_{i=1}^n h_i = P\)), то:
\(
S_{\text{боковой}} = x \cdot P
\)
Ответ:
\(S_{\text{боковой}} = P \cdot x\).
Дано, что наклонная призма имеет боковые грани, каждая из которых представляет собой параллелограмм. Необходимо доказать, что площадь боковой поверхности призмы \(S_{\text{боковой}}\) равна произведению периметра перпендикулярного сечения \(P\) на длину боковой грани \(x\).
Рассмотрим, что площадь боковой поверхности призмы \(S_{\text{боковой}}\) состоит из суммы площадей всех боковых граней. Обозначим площадь каждой боковой грани как \(S_i\), где \(i\) — номер грани. Тогда:
\(S_{\text{боковой}} = \sum_{i=1}^n S_i\)
Каждая боковая грань является параллелограммом, площадь которого вычисляется как произведение длины боковой грани \(x\) на высоту этой грани \(h_i\). Следовательно:
\(S_i = x \cdot h_i\)
Подставим выражение для \(S_i\) в формулу для \(S_{\text{боковой}}\):
\(S_{\text{боковой}} = \sum_{i=1}^n (x \cdot h_i)\)
Так как \(x\) — длина боковой грани, она одинакова для всех боковых граней призмы и является постоянной величиной. Поэтому \(x\) можно вынести за знак суммы:
\(S_{\text{боковой}} = x \cdot \sum_{i=1}^n h_i\)
Теперь рассмотрим сумму высот всех боковых граней \(\sum_{i=1}^n h_i\). Эта сумма равна периметру перпендикулярного сечения призмы \(P\), так как каждая высота \(h_i\) соответствует стороне перпендикулярного сечения. Таким образом:
\(\sum_{i=1}^n h_i = P\)
Подставим это значение в формулу для \(S_{\text{боковой}}\):
\(S_{\text{боковой}} = x \cdot P\)
Таким образом, доказано, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения \(P\) на длину боковой грани \(x\).
Ответ: \(S_{\text{боковой}} = P \cdot x\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!