ГДЗ по Геометрии 10 класс Номер 235 Атанасян — Подробные Ответы

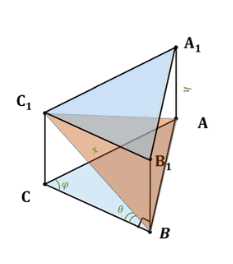
Основанием прямой призмы является прямоугольный треугольник с острым углом \(\varphi\). Через катет, противолежащий этому углу, и через противоположную этому катету вершину основания проведено сечение, составляющее угол \(\theta\) с плоскостью основания. Найдите отношение площади боковой поверхности призмы к площади сечения.

Дано:
Призма \(ABCA_1B_1C_1\),
\(\angle ABC = 90^\circ\),
\(\angle ABC = \varphi\),
\(\angle (ABC, ABC_1) = \theta\).

Найти: \(\frac{S_{\text{боковой}}}{S_{\text{сечения}}}\).

Решение:
Обозначим:
\(AC = x\), \(AA_1 = h\).

Площадь боковой поверхности:
\(
S_{\text{боковой}} = P_{ABC} \cdot h = (x + x \cdot \cos(\varphi) + x \cdot \sin(\varphi)) \cdot h = \)
\(=x \cdot h \cdot (1 + \cos(\varphi) + \sin(\varphi)).
\)

Площадь сечения:
\(
S_{\text{сечения}} = \frac{1}{2} \cdot AB \cdot h_{\text{сечения}} = \frac{1}{2} \cdot x \cdot \sin(\varphi) \cdot \frac{h}{2 \cdot \sin(\theta)} = \frac{x \cdot h \cdot \sin(\varphi)}{2 \cdot \sin(\theta)}.
\)

Отношение:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{x \cdot h \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\frac{x \cdot h \cdot \sin(\varphi)}{2 \cdot \sin(\theta)}} = \frac{2 \cdot \sin(\theta) \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\sin(\varphi)}.
\)

Ответ:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{2 \cdot \sin(\theta) \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\sin(\varphi)}.
\)

Дано прямоугольная призма \(ABCA_1B_1C_1\), у которой \(\angle ABC = 90^\circ\), \(\angle ABC = \varphi\), \(\angle (ABC, ABC_1) = \theta\). Требуется найти отношение площади боковой поверхности призмы к площади сечения, проведенного через ребро \(AB\) и точку \(C_1\).

Обозначим длину основания \(AC = x\) и высоту призмы \(AA_1 = h\).

Для нахождения площади боковой поверхности призмы \(S_{\text{боковой}}\), воспользуемся формулой:
\(
S_{\text{боковой}} = P_{ABC} \cdot h,
\)
где \(P_{ABC}\) — периметр треугольника \(ABC\). Периметр треугольника равен сумме его сторон:
\(
P_{ABC} = AC + BC + AB.
\)
Поскольку \(\angle ABC = 90^\circ\), то \(BC = AC \cdot \cos(\varphi)\), а \(AB = AC \cdot \sin(\varphi)\). Значит,
\(
P_{ABC} = x + x \cdot \cos(\varphi) + x \cdot \sin(\varphi).
\)
Тогда площадь боковой поверхности:
\(
S_{\text{боковой}} = h \cdot (x + x \cdot \cos(\varphi) + x \cdot \sin(\varphi)) = x \cdot h \cdot (1 + \cos(\varphi) + \sin(\varphi)).
\)

Теперь найдем площадь сечения \(S_{\text{сечения}}\). Сечение представляет собой треугольник, основание которого равно \(AB\), а высота проведена из точки \(C_1\) перпендикулярно плоскости \(AB\). Высота треугольника \(h_{\text{сечения}}\) связана с углом \(\theta\) следующим образом:
\(
h_{\text{сечения}} = \frac{h}{2 \cdot \sin(\theta)}.
\)
Основание треугольника \(AB = x \cdot \sin(\varphi)\). Тогда площадь сечения:
\(
S_{\text{сечения}} = \frac{1}{2} \cdot AB \cdot h_{\text{сечения}} = \frac{1}{2} \cdot x \cdot \sin(\varphi) \cdot \frac{h}{2 \cdot \sin(\theta)} = \frac{x \cdot h \cdot \sin(\varphi)}{2 \cdot \sin(\theta)}.
\)

Теперь найдем отношение площадей:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{x \cdot h \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\frac{x \cdot h \cdot \sin(\varphi)}{2 \cdot \sin(\theta)}}.
\)
Упростим выражение:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{x \cdot h \cdot (1 + \cos(\varphi) + \sin(\varphi)) \cdot 2 \cdot \sin(\theta)}{x \cdot h \cdot \sin(\varphi)}.
\)
Сокращая одинаковые множители (\(x\), \(h\)), получаем:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{2 \cdot \sin(\theta) \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\sin(\varphi)}.
\)

Таким образом, отношение площадей равно:
\(
\frac{S_{\text{боковой}}}{S_{\text{сечения}}} = \frac{2 \cdot \sin(\theta) \cdot (1 + \cos(\varphi) + \sin(\varphi))}{\sin(\varphi)}.
\)